Intervals in Mathematics

An interval is a set of numbers or points that lie between two values, a and b, known as the endpoints of the interval, where a < b.

Open and Closed Intervals

An interval may be:

• closed [a,b], if it includes both endpoints:
  $$ [a,b] = \{ x \in R: a \le x \le b \} $$
  
• open (a,b), if it excludes both endpoints:
  $$ (a,b) = \{ x \in R: a < x < b \} $$
  

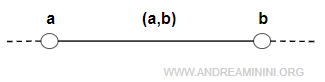
Note. The values a and b are referred to as the endpoints, whether the interval is open or closed.

An interval can also be:

• open on the left and closed on the right (a,b], meaning that b is included in the interval, while a is not:
  $$ (a,b] = \{ x \in R: a < x \le b \} $$
  
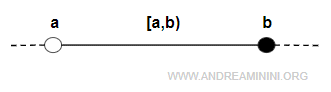
• closed on the left and open on the right [a,b), meaning that a is included but b is not:
  $$ (a,b] = \{ x \in R: a \le x < b \} $$
  

Bounded and Unbounded Intervals

An interval can be either bounded or unbounded:

• bounded interval, if both endpoints a and b are finite numbers:
  $$ (a,b) $$
• unbounded interval, if at least one endpoint is ±∞:
  $$ (a,+\infty) \\ (-\infty, b) \\ (-\infty,+\infty) = R $$
  

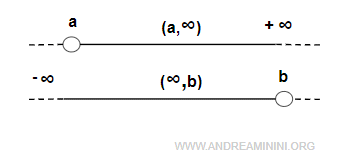
Note. In unbounded intervals, infinity is always considered an open endpoint because it’s not an actual number but a symbol that represents an endless range of values. Depending on the case, an unbounded interval may lack an upper bound, a lower bound, or both - for instance, (a,+∞) or (-∞,b). Conversely, the finite endpoint of an unbounded interval can be either closed, as in [a,+∞) or (-∞,b], or open, as in (a,+∞) or (-∞,b).

And so on.