Algebraic Fractions
What is an algebraic fraction?
An algebraic fraction is the ratio of two polynomials A and B: $$ \frac{A}{B} $$ where B is a nonzero polynomial.
For example, the ratio of the polynomials x+1 and x-1 is an algebraic fraction:
$$ \frac{x+1}{x-1} $$
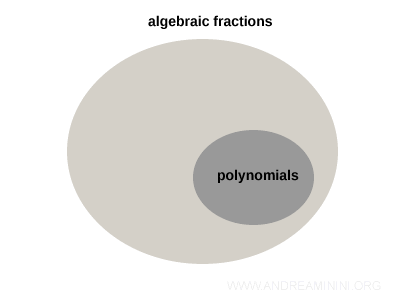
The set of algebraic fractions is far broader than the set of polynomials because:
- Every polynomial can be seen as a special case of an algebraic fraction.
Note. Any polynomial can be written as a ratio with denominator 1. For instance, the polynomial x+1 can be expressed as: $$ P = x+1 = \frac{x+1}{1} $$
- The quotient of two polynomials is always an algebraic fraction, though not necessarily a polynomial.
Note. The division of two polynomials produces a polynomial only if the remainder is zero (R=0). That is, only when the numerator is exactly divisible by the denominator. For example, the fraction $$ \frac{x+1}{x-1} $$ is not a polynomial, because dividing (x+1) by (x-1) leaves a nonzero remainder (R=2).

We can therefore conclude that every polynomial is an algebraic fraction, but not every algebraic fraction is a polynomial.
In other words, the set of polynomials is a proper subset of the set of algebraic fractions.
The Condition of Existence
An algebraic fraction is defined only for values of the variable(s) that do not make the denominator vanish, since division by zero is undefined in mathematics.
This restriction is known as the condition of existence, usually abbreviated as C.E.
Example. The algebraic fraction $$ \frac{x+1}{x-1} $$ is defined for all real values of x except $x = 1$, which makes the denominator equal to zero. The condition of existence is therefore: $$ \text{C.E.} \quad x \ne 1 $$
A Practical Example
Consider the algebraic fraction:
$$ \frac{x+1}{x \cdot (x-1)} $$
This fraction is defined for all real values of x except $x = 0$ and $x = 1$.
If $x = 0$ or $x = 1$, the denominator vanishes by the zero-product property.
Thus, the condition of existence is:
$$ \text{C.E.} \quad x \ne 0 \ \wedge \ x \ne 1 $$
And so forth.
