Compositions in Symmetric Groups

A composition is the operation that combines the bijective correspondences of two symmetric groups within the same reference set X.

In simpler terms, a composition is the outcome of multiplying two permutations together.

Example

Consider a set X

$$ X = ( 1, 2, 3, 4, 5 ) $$

and two bijective correspondences

$$ \sigma:X \rightarrow X $$

$$ t:X \rightarrow X $$

where

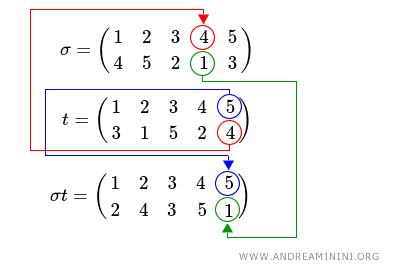
$$ \sigma = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 5 & 2 & 1 & 3 \end{pmatrix} $$

$$ t = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 3 & 1 & 5 & 2 & 4 \end{pmatrix} $$

The composition σ * t is

$$ \sigma * t = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 4 & 1 & 3 & 5 \end{pmatrix} $$

For the sake of brevity, from now on I will write σ * t using the notation σt without indicating the operator symbol.

Explanation. Being a composition of the type f[g(x)], or σ[t(x)], I must first compute the inner permutation t (the second) and then the outer permutation σ (the first).

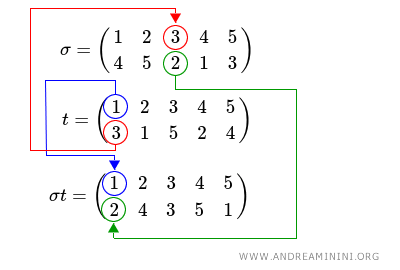
After determining the transition of the first element in the permutation t, I proceed sequentially to the second element of permutation t.

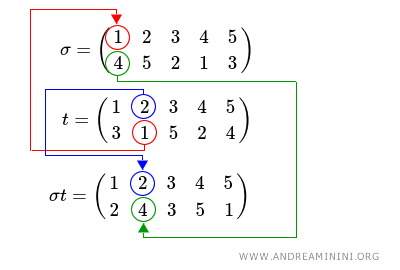
Then to the third element of permutation t and so on, until a new position has been assigned to each element.

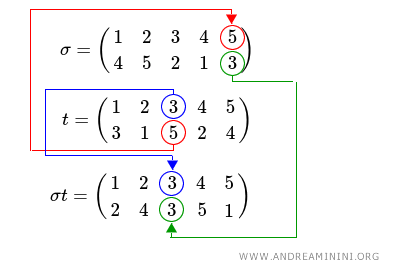
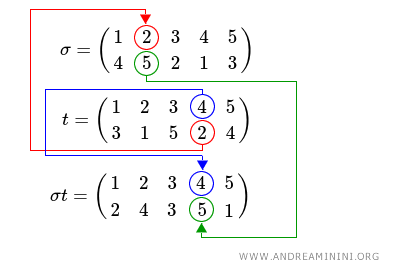
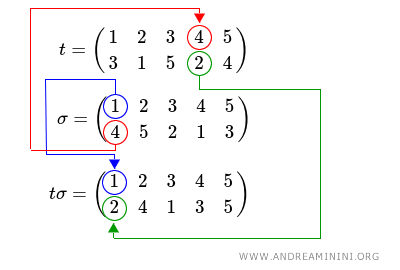
Composition is a non-abelian operation because it does not respect the commutative property.

Switching the order of the permutations results in a different composition.

$$ t\sigma = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 4 & 1 & 3 & 5 \end{pmatrix} $$

To save time, I will only demonstrate the first result rather than going through all the steps to achieve the latter result.

Note. Only if n ≤ 2, meaning if there are two or just one element in set X, is the composition an abelian (commutative) operation. For instance, consider these two permutations with two elements each: $$ \sigma = \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} $$ $$ t = \begin{pmatrix} 1 & 2 \\ 1 & 2 \end{pmatrix} $$ The result of the composition σt $$ \sigma t = \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} $$ is the same as obtained in the composition tσ $$ t \sigma = \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} $$ Hence, the operation satisfies the commutative property.

And so on.