Derivative of a Function

What Is a Derivative?

The derivative of a function f(x) at a point x is defined as the limit of the difference quotient:

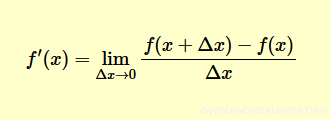
This limit is called the first derivative and is denoted by f'(x).

The process of taking this limit is known as differentiation.

Example

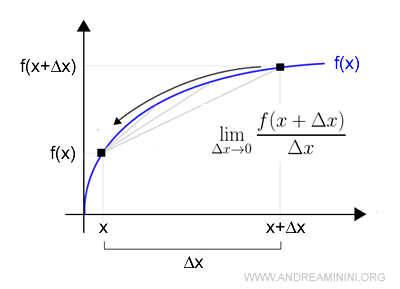
The first derivative can also be expressed using alternative notations:

$$ f'(x)=Df=\frac{dy}{dx}=y' $$

The expression dy/dx is called Leibniz’s notation.

Note. The first derivative f'(x) is itself a function and can be differentiated again. The derivative of the derivative is called the second derivative, denoted by f''(x), and so on.

Conditions for Differentiability

A function f(x), defined on an interval (a, b), is said to be differentiable at a point x if the limit of the difference quotient exists as h approaches zero.

 

A function is differentiable over an open interval (a, b) if it is differentiable at every point x strictly between a and b - that is, for all x ∈ (a, b).

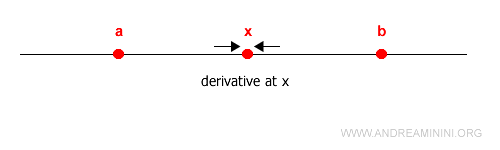
A function is differentiable over a closed interval [a, b] if it is differentiable at every point x ∈ [a, b], and if the right-hand derivative exists at x = a and the left-hand derivative exists at x = b.

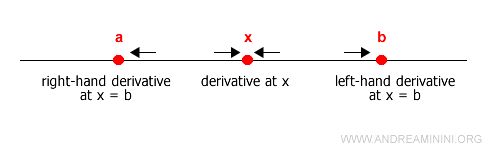
Points at which a function fails to be differentiable are called singular points.

Left and Right Derivatives

Sometimes, a function may not be differentiable at a particular point x, but it may still be differentiable on either side of x.

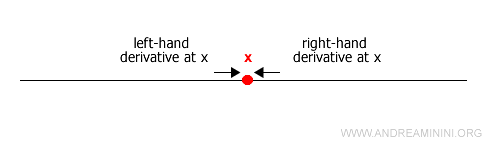
In such cases, the finite limits taken from the left and the right are referred to as the left-hand derivative and the right-hand derivative at x, respectively.

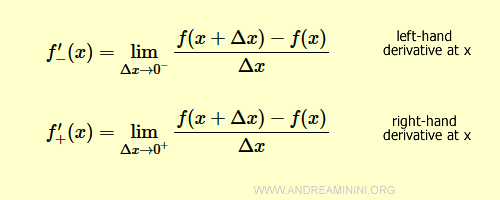
What’s the difference?

For the left-hand derivative, the increment Δx approaches 0 from the negative side, meaning Δx < 0.

For the right-hand derivative, Δx approaches 0 from the positive side, so Δx > 0.

If a function is differentiable at x, then both the left-hand and right-hand derivatives exist and are equal: $$ f'(x) = f'_-(x) = f'_+(x) $$

A Practical Example

Consider the function:

$$ \frac{1}{x} $$

This function is undefined at x = 0 and therefore not differentiable at that point.

So, x = 0 is a singular point of f(x).

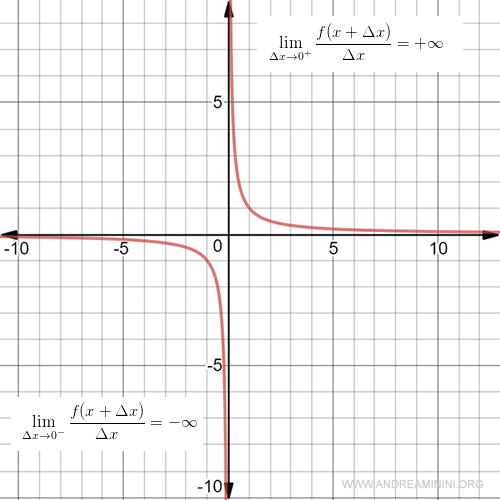
However, the function still has both a left-hand and a right-hand derivative at x = 0.

The left-hand derivative tends toward negative infinity:

$$ f'_-(x) = \lim_{Δx \rightarrow 0^-} \frac{f(x+Δx)-f(x)}{Δx} = - \infty $$

The right-hand derivative tends toward positive infinity:

$$ f'_+(x) = \lim_{Δx \rightarrow 0^+} \frac{f(x+Δx)-f(x)}{Δx} = + \infty $$

Analyzing one-sided limits like these helps us understand how a function behaves even at points where it’s not defined.

Derivative Corollaries

• If a function is differentiable at x and its derivative f'(x) is finite, then the left-hand and right-hand derivatives not only exist, but are equal to the derivative:

  $$ \text{If} \:\: f'(x) = l \:\Rightarrow \: f'(x) = f'_-(x) = f'_+(x) $$

  On the other hand, if the function is not differentiable at x, then the left-hand and right-hand derivatives may differ or one of them might not exist at all.

Leibniz Notation

One of the most common notations used in calculus is Leibniz's notation.

$$ \frac{dy}{dx} $$ or $$ \frac{δy}{δx} $$

The numerator represents the dependent variable (the function’s output).

The denominator specifies the independent variable with respect to which the differentiation is performed.

Note. Leibniz’s notation is especially helpful when dealing with functions of multiple variables and it’s important to indicate which variable you're differentiating with respect to. If only one variable is involved, it’s often more convenient to use a more compact notation such as y''.

And so on.