Logarithmic Equations

A logarithmic equation is an equation in which the unknown variable appears inside the argument of at least one logarithm. $$ \log_b P(x) = \log_b Q(x) $$ Here, P and Q are polynomials or more general functions of x.

There are two main strategies commonly used to solve logarithmic equations.

Method 1

1. determine the domain where each logarithm is defined
2. solve the equation between the arguments, that is, solve P(x)=Q(x)
3. discard any candidate solutions that violate the domain conditions

Method 2

1. introduce an auxiliary variable, for example u=log(x)
2. solve the resulting equation in the new variable u
3. solve each logarithmic equation of the form log(x)=s
4. eliminate the solutions that fall outside the admissible domain

Note. The equation below is logarithmic because the unknown appears inside the logarithmic argument $$ 3 \log(x) = 2 $$ In contrast, the next equation is not logarithmic, since the variable does not occur inside a logarithm. $$ (x-1) \log(3) = 5 $$

A Practical Example

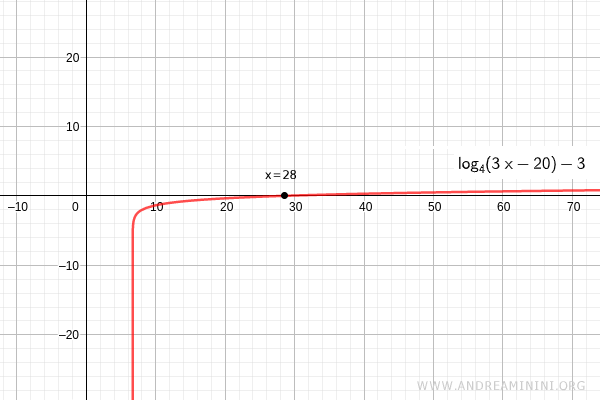
Consider the logarithmic equation

$$ \log_4 (3x-20) = 3 $$

We begin by determining the domain of definition of the logarithm. Its argument must be positive.

$$ 3x - 20 > 0 $$

Thus the variable must satisfy

$$ x > \frac{20}{3} $$

We now exponentiate both sides using base 4.

$$ 4^{\log_4 (3x-20)} = 4^3 $$

$$ 4^{\log_4 (3x-20)} = 64 $$

Since exponentiation is the inverse operation of the logarithm, the expression simplifies to

$$ 3x - 20 = 64 $$

$$ 3x = 64 + 20 $$

$$ x = \frac{84}{3} $$

We obtain the value

$$ x = 28 $$

This is a valid solution of the logarithmic equation because it satisfies the condition x>20/3.

Example 2

Now solve the following logarithmic equation using the auxiliary variable method:

$$ \log_2 x^2 + \log_2^2 x = 0 $$

Rewrite it in a clearer form:

$$ \log_2 x^2 + ( \log_2 x )^2 = 0 $$

The domain condition is simply x>0.

$$ \begin{cases} x^2 > 0 \\ \\ x > 0 \end{cases} \Rightarrow x > 0 $$

To apply the auxiliary variable method, both logarithms must share the same base and the same argument.

Using the power rule for logarithms, bring down the exponent from x²:

$$ 2 \cdot \log_2 x + ( \log_2 x )^2 = 0 $$

Now the logarithmic terms are expressed in a uniform way.

Introduce the auxiliary variable u = \log_2 x.

$$ 2u + u^2 = 0 $$

This converts the problem into a quadratic equation.

$$ u (u + 2) = 0 $$

The solutions are u=0 and u=-2.

$$ u = \begin{cases} 0 \\ \\ -2 \end{cases} $$

Substitute back u = log₂ x:

$$ \log_2 x = \begin{cases} 0 \\ \\ -2 \end{cases} $$

We now solve these logarithmic equations.

The first gives x₁=2⁰=1.

$$ \log_2 x = 0 \Rightarrow 2^0 = 1 $$

This value is admissible for the original equation because it satisfies x>0.

The second gives x₂=2^-2=1/4.

$$ \log_2 x = -2 \Rightarrow 2^{-2} = \frac{1}{4} $$

This value also satisfies the condition x>0, so it is acceptable.

Therefore, the solutions of the logarithmic equation are x₁=1 and x₂=1/4.

 

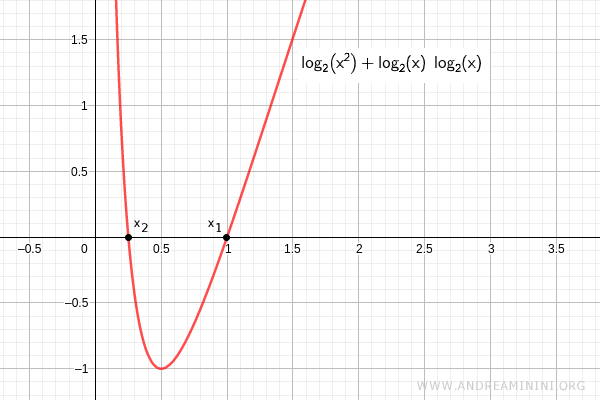
Derivation and Explanation

Logarithms are defined only when their arguments are positive.

$$ P(x) > 0 $$

$$ Q(x) > 0 $$

This requirement forms the domain of definition of the logarithm.

Consequently, a logarithmic equation may have solutions only if these domain conditions are satisfied.

The key principle for solving logarithmic equations is the equivalence

$$ P(x) = Q(x) \Leftrightarrow \log_b P(x) = \log_b Q(x) $$

Explanation. By the invariance property of equations, we may exponentiate both sides: $$ \log_b P(x) = \log_b Q(x) $$ $$ b^{\log_b P(x)} = b^{\log_b Q(x)} $$ Since exponentiation is the inverse of the logarithm, we obtain $$ P(x) = Q(x) $$

Thus, solving a logarithmic equation reduces to solving the equation between the arguments

$$ P(x) = Q(x) $$

and then discarding any solutions that violate the domain conditions.

And so on.