Maclaurin Series

The Maclaurin series (sometimes spelled McLaurin) is a formula used to approximate the behavior of a function near the point x₀ = 0. $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(0)}{k!} \cdot x^k + o(x^n) $$

The resulting polynomial serves as an n-th order approximation of the function f(x) around zero.

The higher the degree n of the Maclaurin polynomial, the more accurately it approximates the function f(x) in the neighborhood of zero.

Note. The Maclaurin series is a special case of the Taylor series where x₀ = 0. $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k + R_n(x) $$

A Practical Example

Consider the exponential function:

$$ f(x) = e^x $$

The graph of the exponential function appears as follows:

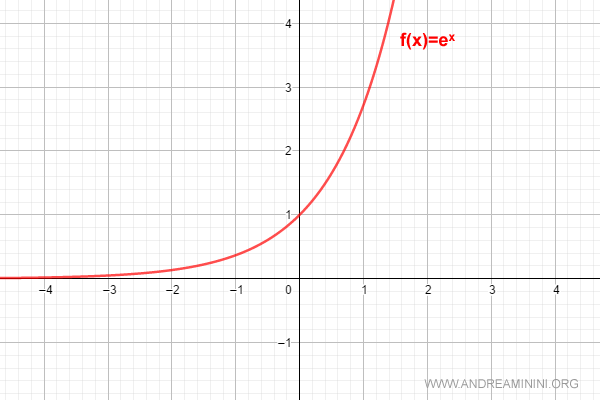
Let’s construct a polynomial that approximates the exponential function using the Maclaurin series:

$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(0)}{k!} \cdot x^k + o(x^n) $$

or equivalently:

$$ P_n(x) = \sum_{k=0}^{n} \frac{D^{(k)}[e^0]}{k!} \cdot x^k + o(x^n) $$

For n = 0, the series reduces to:

$$ P_0(x) = \sum_{k=0}^{0} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 $$

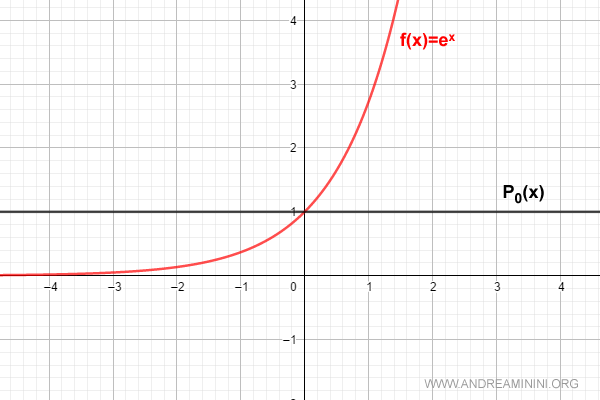
For n = 1, we obtain:

$$ f(x) = \sum_{k=0}^{1} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x $$

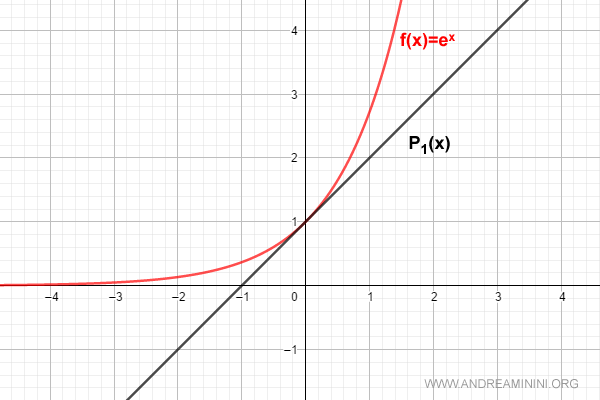
For n = 2, the series becomes:

$$ f(x) = \sum_{k=0}^{2} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x + \frac{x^2}{2!} $$

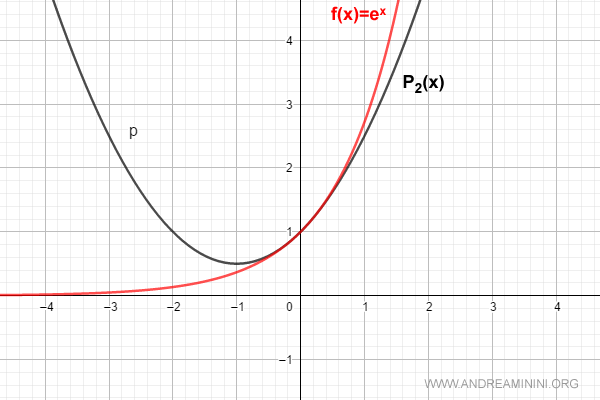
For n = 3, we get:

$$ f(x) = \sum_{k=0}^{3} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} $$

As the degree of the polynomial increases, the Maclaurin series offers a progressively more precise approximation of the function near x₀ = 0.

For instance, with n = 9, the polynomial approximates the function extremely well around zero:

$$ f(x) = \sum_{k=0}^{9} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots + \frac{x^9}{9!} $$

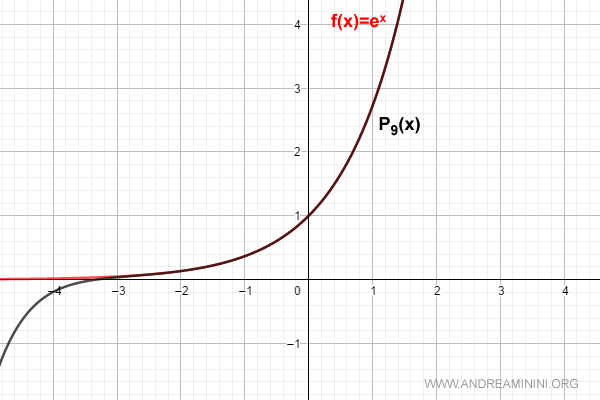
Thus, for any positive integer n, the polynomial takes the form:

$$ f(x) = \sum_{k=0}^{n} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots + \frac{x^n}{n!} $$

And so forth.