Taylor’s Formula

Taylor’s formula provides an approximation of a function f(x) that is differentiable n times in a neighborhood of a point x₀ ∈ ℝ, using a polynomial of degree n along with a remainder term R. $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x-x_0)^k + R_n(x) $$ where $$ \lim_{x \rightarrow x_0} \frac{R_n}{(x-x_0)^n} = 0 $$

This polynomial is called the Taylor Polynomial of f(x) at x₀, of degree (or order) n.

The higher the degree n, the more accurately the polynomial approximates the function.

As n approaches infinity, the remainder term R tends to zero:

$$ \lim_{n \rightarrow \infty} R_n = 0 $$

Why is it useful? Taylor’s formula enables us to express a function f(x) as an algebraic polynomial P(x). This form often makes it easier and more efficient to analyze the function’s properties and behavior.

A Worked Example

Let’s consider the exponential function:

$$ f(x) = e^x $$

We’ll expand it around the point x₀ = 0:

$$ x_0 = 0 $$

At this point, the function evaluates to:

$$ f(0) = e^0 = 1 $$

Since all derivatives of e^x are equal to e^x, we have:

$$ D[e^x] = e^x $$

Therefore, for any integer k:

$$ f^{(k)}(0) = 1 $$

Hence, the Taylor polynomial of degree n = 2 is:

$$ f(x) = \frac{f^{(0)}(x_0)}{0!} \cdot (x - x_0)^0 + \frac{f^{(1)}(x_0)}{1!} \cdot (x - x_0)^1 + \frac{f^{(2)}(x_0)}{2!} \cdot (x - x_0)^2 + R_2 $$

$$ f(x) = \frac{D^{(0)}[e(x_0)]}{0!} \cdot (x - x_0)^0 + \frac{D^{(1)}[e(x_0)]}{1!} \cdot (x - x_0)^1 + \frac{D^{(2)}[e(x_0)]}{2!} \cdot (x - x_0)^2 + R_2 $$

Recalling that the zeroth derivative is simply the function itself, we get:

$$ f(x) = \frac{e(x_0)}{0!} \cdot (x - x_0)^0 + \frac{D^{(1)}[e(x_0)]}{1!} \cdot (x - x_0)^1 + \frac{D^{(2)}[e(x_0)]}{2!} \cdot (x - x_0)^2 + R_2 $$

Substituting x₀ = 0 gives:

$$ f(x) = \frac{e(0)}{0!} \cdot (x - 0)^0 + \frac{D^{(1)}[e(0)]}{1!} \cdot (x - 0)^1 + \frac{D^{(2)}[e(0)]}{2!} \cdot (x - 0)^2 + R_2 $$

$$ f(x) = \frac{e(0)}{0!} \cdot x^0 + \frac{D^{(1)}[e(0)]}{1!} \cdot x^1 + \frac{D^{(2)}[e(0)]}{2!} \cdot x^2 + R_2 $$

Given that every k-th derivative of e^x is still e^x, we have:

$$ f(x) = \frac{e(0)}{0!} \cdot x^0 + \frac{e(0)}{1!} \cdot x^1 + \frac{e(0)}{2!} \cdot x^2 + R_2 $$

Since e⁰ = 1:

$$ f(x) = \frac{1}{0!} \cdot x^0 + \frac{1}{1!} \cdot x^1 + \frac{1}{2!} \cdot x^2 + R_2 $$

Evaluating the factorials in the denominators (with 0! defined as 1) yields:

$$ f(x) = \frac{1}{1} \cdot x^0 + \frac{1}{1} \cdot x^1 + \frac{1}{2} \cdot x^2 + R_2 $$

$$ f(x) = \frac{x^0}{1} + \frac{x^1}{1} + \frac{x^2}{2} + R_2 $$

$$ f(x) = 1 + x + \frac{x^2}{2} + R_2 $$

Even though this Taylor polynomial is only of degree 2, it already provides a reasonably good approximation of the function f(x) = e^x.

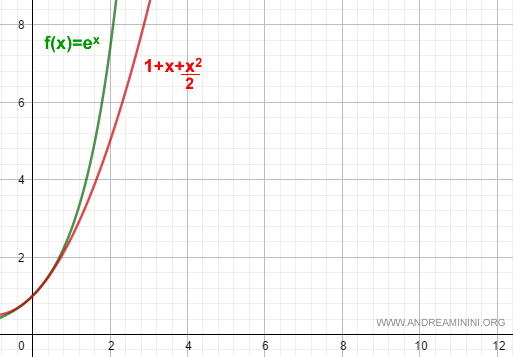
By increasing the degree of the polynomial to k + 1 = 3, the approximation becomes even more precise:

$$ f(x) = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + R_3 $$

This new third-degree polynomial fits the graph of the function more closely than the previous second-degree polynomial (shown as a dotted curve).

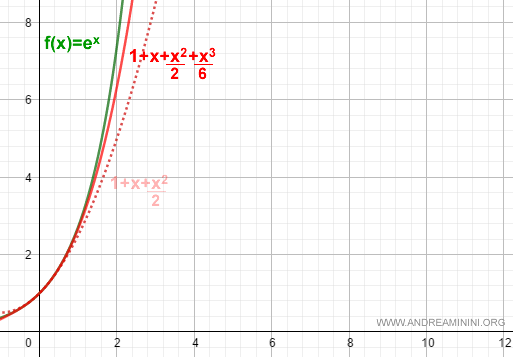
Thus, the remainder term of the Taylor polynomial approaches zero as k approaches infinity:

$$ \lim_{k \rightarrow \infty} R_k = 0 $$

Proof

Assume that the n-th derivative f(n)(x) is continuous at x₀.

We aim to show that the remainder term in Taylor’s formula approaches zero as x tends toward x₀:

$$ \lim_{x \rightarrow x_0} \frac{R_n}{(x - x_0)^n} = 0 $$

By definition, the remainder R is the difference between the function f(x) and its Taylor polynomial:

$$ R_n = f(x) - P(x) $$

$$ R_n = f(x) - \left[ f(x_0) + f'(x_0)(x - x_0) + \dots + \frac{f^{(n)}(x_0)(x - x_0)^n}{n!} \right] $$

Substituting R into the limit yields:

$$ \lim_{x \rightarrow x_0} \frac{f(x) - \left[ f(x_0) + f'(x_0)(x - x_0) + \dots + \frac{f^{(n)}(x_0)(x - x_0)^n}{n!} \right]}{(x - x_0)^n} = \frac{0}{0} $$

Note. The numerator becomes zero because f(x) and its Taylor polynomial coincide at x₀. The denominator tends to zero as x approaches x₀. This explains why the limit takes the indeterminate form 0/0.

To resolve this indeterminate form, we apply L’Hôpital’s Theorem.

We differentiate both the numerator and denominator with respect to x:

$$ \lim_{x \rightarrow x_0} \frac{D \left[ f(x) - \left( f(x_0) + f'(x_0)(x - x_0) + \dots + \frac{f^{(n)}(x_0)(x - x_0)^n}{n!} \right) \right]}{D \left[ (x - x_0)^n \right]} $$

$$ \lim_{x \rightarrow x_0} \frac{ f'(x) - \left[ f'(x_0) + f''(x_0)(x - x_0) + \dots + \frac{f^{(n)}(x_0)(x - x_0)^{n - 1}}{(n - 1)!} \right] }{ n \cdot (x - x_0)^{n - 1} } = \frac{0}{0} $$

Since this remains an indeterminate form, we continue applying L’Hôpital’s Theorem, differentiating numerator and denominator a total of n times.

After n differentiations, we obtain:

$$ \lim_{x \rightarrow x_0} \frac{f^{(n)}(x) - f^{(n)}(x_0)}{n!} $$

Because f(x) is continuous at x₀, the numerator approaches zero as x → x₀ since f^{(n)}(x) - f^{(n)}(x_0) → 0.

The denominator is the constant n!, the factorial of the polynomial’s degree.

Thus, the limit evaluates to zero:

$$ \lim_{x \rightarrow x_0} \frac{f^{(n)}(x) - f^{(n)}(x_0)}{n!} = 0 $$

Hence, the original limit also equals zero:

$$ \lim_{x \rightarrow x_0} \frac{ f'(x) - \left[ f'(x_0) + f''(x_0)(x - x_0) + \dots + \frac{f^{(n)}(x_0)(x - x_0)^{n - 1}}{(n - 1)!} \right] }{ n \cdot (x - x_0)^{n - 1} } = 0 $$

which establishes that:

$$ \lim_{x \rightarrow x_0} \frac{R_n}{(x - x_0)^n} = 0 $$

This completes the proof of Taylor’s formula.

Peano’s Remainder

Peano’s remainder is defined as the difference between the Taylor polynomial p_n of degree n, centered at x₀, and the function f(x) being approximated: $$ R_n(x) = f(x) - p_n(x) $$

Peano’s remainder quantifies the error in approximating f(x) by its Taylor polynomial:

$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k + R_n(x) $$

The Taylor polynomial p_n(x) is given by:

$$ p_n(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k $$

Hence, by straightforward algebraic rearrangement:

$$ f(x) = p_n(x) + R_n(x) $$

$$ f(x) - p_n(x) = R_n(x) $$

Thus, Peano’s remainder R precisely represents the difference between the function f(x) and its Taylor polynomial p_n(x) of degree n centered at x₀.

Peano’s remainder R_n(x) is said to be of higher order than (x - x₀)ⁿ if f(x) is differentiable up to order n at x₀: $$ \lim_{x \rightarrow x_0} \frac{R_n(x)}{(x - x_0)^n} = 0 $$

The Proof

$$ \lim_{x \rightarrow x_0} \frac{R_n(x)}{(x - x_0)^n} $$

Since R_n(x) = f(x) - p_n(x):

$$ \lim_{x \rightarrow x_0} \frac{f(x) - p_n(x)}{(x - x_0)^n} $$

We substitute p_n(x) with its Taylor expansion:

$$ \lim_{x \rightarrow x_0} \frac{f(x) - \left[ f(x_0) + f'(x_0)(x - x_0) + \dots + \frac{f^{(n)}(x_0)(x - x_0)^n}{n!} \right]}{(x - x_0)^n} $$

This limit also yields an indeterminate form of type 0/0.

To evaluate it, we apply L’Hôpital’s Theorem repeatedly (n - 1 times):

$$ \lim_{x \rightarrow x_0} \frac{f^{(n-1)}(x) - \left[ f^{(n-1)}(x_0) + f^{(n)}(x_0)(x - x_0) \right]}{n! \cdot (x - x_0)} $$

We can factor out 1/n! from the limit:

$$ \frac{1}{n!} \lim_{x \rightarrow x_0} \frac{f^{(n-1)}(x) - \left[ f^{(n-1)}(x_0) + f^{(n)}(x_0)(x - x_0) \right]}{(x - x_0)} $$

$$ \frac{1}{n!} \lim_{x \rightarrow x_0} \frac{f^{(n-1)}(x) - f^{(n-1)}(x_0) - f^{(n)}(x_0)(x - x_0)}{(x - x_0)} $$

Separating terms and simplifying:

$$ \frac{1}{n!} \lim_{x \rightarrow x_0} \left[ \frac{f^{(n-1)}(x) - f^{(n-1)}(x_0)}{(x - x_0)} - \frac{f^{(n)}(x_0)(x - x_0)}{(x - x_0)} \right] $$

$$ \frac{1}{n!} \lim_{x \rightarrow x_0} \left[ \frac{f^{(n-1)}(x) - f^{(n-1)}(x_0)}{(x - x_0)} - f^{(n)}(x_0) \right] $$

We may split the limit into separate terms:

$$ \frac{1}{n!} \left[ \lim_{x \rightarrow x_0} \frac{f^{(n-1)}(x) - f^{(n-1)}(x_0)}{(x - x_0)} - \lim_{x \rightarrow x_0} f^{(n)}(x_0) \right] $$

Applying L’Hôpital’s Theorem to the first limit gives f⁽ⁿ⁾(x):

$$ \frac{1}{n!} \cdot \left[ f^{(n)}(x_0) - f^{(n)}(x_0) \right] $$

$$ \frac{1}{n!} \cdot 0 $$

$$ = 0 $$

Note. Peano’s remainder R_n(x) is an infinitesimal of higher order than (x - x₀)ⁿ: $$ \lim_{x \rightarrow x_0} \frac{R_n(x)}{(x - x_0)^n} = 0 $$ Consequently, in Taylor’s polynomial, we can express it using the little-o notation: $$ R_n(x) = o\bigl((x - x_0)^n\bigr) $$ which yields: $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k + o\bigl((x - x_0)^n\bigr) $$

Taylor’s Formula in Alternative Notation

If Peano’s remainder is of order o((x - x₀)ⁿ), Taylor’s formula can also be expressed in this alternative form:

$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k + o\bigl((x - x_0)^n\bigr) $$

Estimating Peano’s Remainder

If f(x) is differentiable (n+1) times in a neighborhood of x₀, and its (n+1)-th derivative is continuous, and if M denotes the maximum value of that derivative in the neighborhood, an estimate for Peano’s remainder is given by: $$ |R_n(x)| \le M \cdot \frac{|x - x_0|^{n+1}}{(n+1)!} $$

Maclaurin’s Formula

Maclaurin’s formula is a special case of Taylor’s formula where x₀ = 0: $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(0)}{k!} \cdot x^k + o\bigl(x^n\bigr) $$

And so on.