Infinitesimals in Mathematics

What is an infinitesimal?

In mathematics, an infinitesimal is a quantity that is infinitely small. The concept of infinitesimals was first introduced by Leibniz and is a fundamental idea in calculus. It is also commonly referred to as "little o".

The infinitesimal function

A function is called an infinitesimal function at x₀ if the limit of f(x) approaches zero as x approaches x₀: $$ \lim_{x \rightarrow x_0} f(x) = 0 $$

In many cases, the term infinitesimal is used informally to refer to an infinitesimal function.

Example

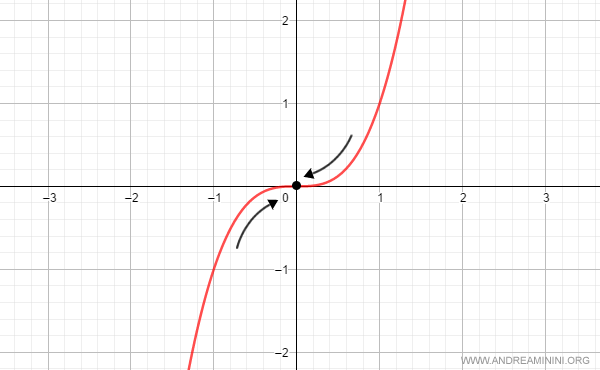
The following function is infinitesimal as x approaches zero:

$$ f(x) = x^3 $$

Although f(x) is nonzero in any neighborhood of x₀,

its limit as x approaches x₀ is zero:

$$ \lim_{x \rightarrow 0} x^3 = 0 $$

Thus, f(x) is an infinitesimal function as x tends to zero.

Higher-order infinitesimals

Let f(x) and g(x) be two functions defined in a neighborhood of x₀ (possibly excluding x₀), and both nonzero for x ≠ x₀. We say that f(x) is a higher-order infinitesimal relative to g(x) as x approaches x₀ if: $$ \lim_{x \rightarrow x_0} \frac{f(x)}{g(x)} = 0 $$

Infinitesimal functions can be compared and ranked, much like infinite functions.

When both f(x) and g(x) approach zero as x → x₀, the function that approaches zero faster is called a higher-order infinitesimal.

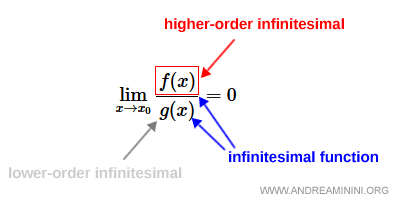
Conversely, g(x) is referred to as a lower-order infinitesimal relative to f(x) as x → x₀.

In this case, the limit of the ratio g(x)/f(x) tends to infinity:

$$ \lim_{x \rightarrow x_0} \frac{g(x)}{f(x)} = \infty $$

Note: The order of infinitesimals can only be established when the infinitesimal functions near x → x₀ can be meaningfully compared. If the limit of the ratio f(x)/g(x) is a finite, nonzero constant, then the two functions are said to be infinitesimals of the same order: $$ \lim_{x \rightarrow x_0} \frac{g(x)}{f(x)} = l $$

Higher-order infinitesimals are closely connected to the mathematical concept known as little o.

Example

Consider two infinitesimal functions f(x) and g(x) as x approaches zero:

$$ f(x) = x^3 $$

$$ g(x) = x^2 $$

Both functions are infinitesimal since their limits are zero as x approaches zero:

$$ \lim_{x \rightarrow 0} x^3 = 0 $$

$$ \lim_{x \rightarrow 0} x^2 = 0 $$

However, they are of different orders of infinitesimal.

This becomes evident when looking at their graphs:

Note: Near x₀ = 0, the function f(x) = x³ (red curve) lies much closer to the x-axis (that is, to zero) than g(x) = x² (blue curve).

If f(x) approaches zero faster than g(x) as x → 0, then the ratio f(x)/g(x) also tends to zero as x → 0:

$$ \lim_{x \rightarrow x_0} \frac{f(x)}{g(x)} = \lim_{x \rightarrow x_0} \frac{x^3}{x^2} = \lim_{x \rightarrow x_0} x = 0 $$

Thus, f(x) is a higher-order infinitesimal compared to g(x) as x → 0.

The meaning of "little o"

If f(x) is a higher-order infinitesimal relative to g(x) as x → x₀, this can also be expressed using the little o notation: $$ f(x) = o(g(x)) \:\:\: \text{as} \: x \rightarrow x_0 $$

Example

Consider two infinitesimal functions as x approaches zero:

$$ f(x) = x^3 $$

$$ g(x) = x^2 $$

Since f(x) is a higher-order infinitesimal relative to g(x) as x approaches zero:

$$ \lim_{x \rightarrow x_0} \frac{f(x)}{g(x)} = 0 $$

We can express this relationship using little o notation:

$$ f(x) = o(g(x)) \:\:\: \text{as} \: x \rightarrow x_0 $$

In other words, f(x) is "little o of g(x)".

And so on.