Mathematical Functions
What is a function?
A function is a specific kind of relation between two sets, A and B, where each element in A (the domain) is paired with one and only one element in B (the codomain). $$ f:A \rightarrow B $$
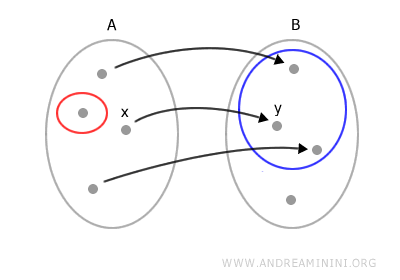
The phrase "one and only one" means that every element in A has a unique corresponding element in B. Here’s an example of a function.
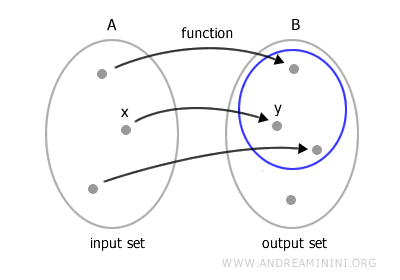
The set A is called the domain, or the set of definition, of the function.
For any element x in A, there exists a unique element y in B, known as the image of x under the function f.
$$ y = f(x) $$
This expression is read as "y equals f of x."
Conversely, the element x is referred to as the preimage of y.
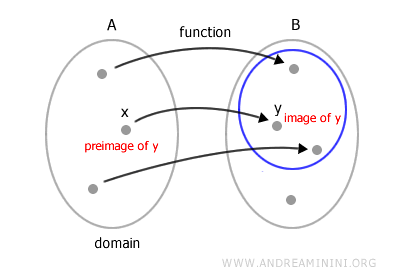
Note. Because each input is associated with exactly one output, the function y = f(x) is also called a mapping, and we say that "f maps x to y". For instance, the function f = x2 takes any real number as input and returns its square. If x = 2, then y = 22 = 4.
Not every element y in B needs to be the image of some element x in A.
The subset C ⊆ B consisting of all the values y = f(x) for x in A is called the codomain of the function.
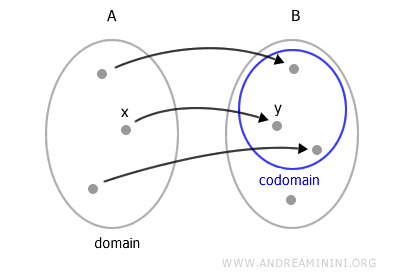
Note. Since the output y depends on the input x, y is called the dependent variable, while x is the independent variable.
Functions are typically denoted by lowercase letters such as f, g, or h.
$$ f:A \rightarrow B $$
Alternatively, for any x ∈ A and y ∈ B, we can write
$$ f:x \longmapsto y $$
A function f is also described as a one-to-one correspondence because each element of the domain is associated with exactly one element in the codomain.
When is a relation not a function? A relation is not a function if a single element in A is associated with more than one element in B.
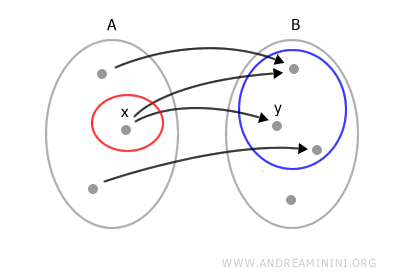
Likewise, a relation is not a function if at least one element in A is not associated with any element in B.
Functions can also depend on two or more independent variables.
$$ y = f(x_1, x_2, ...) $$
In this case, the independent variables inside the parentheses - x1, x2, etc. - are called the arguments of the function.
Even with multiple inputs, a function still produces a single output - that is, it has one dependent variable.
Domain of a Function
The domain of a function is the set of all permissible values of the independent variable x - that is, all the values for which the function is defined.
For instance, the following real-valued function is defined for every real number except zero:
$$ \frac{1}{x} $$
Division by zero is undefined in mathematics.
Therefore, the domain of this function is the set of all real numbers excluding zero:
$$ R- \{0 \} $$
In other words, it’s the set of real numbers R, minus zero.
Explicit vs. Implicit Functions
A mathematical function can be written in either explicit or implicit form.
- Explicit form
In explicit form, the function is written as y = f(x), for example: $$ y = x + 1 $$ - Implicit form
In implicit form, the function is expressed by an equation involving both variables, typically written as F(x, y) = 0, for example: $$ y - x - 1 = 0 $$
A function can also be represented as a set of ordered pairs (x, y), where x ∈ A and y ∈ B, such that each value of x appears exactly once.
$$ f:A \rightarrow B $$
In other words, for every a ∈ A, the function f assigns exactly one b ∈ B.
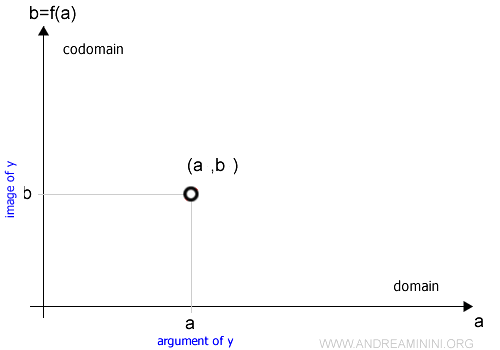
$$ b = f(a) $$
In the ordered pair (a, b), the element a is called the input or argument of f, and b is the output, or the image of a under f (also referred to as the value of f at a).
$$ (a,b)_f = (a,f(a)) $$
Each pair (a, b) can be plotted on the Cartesian plane, in what is called the Cartesian representation of the function.
The set F of all such ordered pairs defined by the function f is called the graph of the function.
This graph is a subset of the Cartesian product A × B.
$$ \{(a, f(a)) \mid a \in A \} \subseteq A \times B $$
Note. Not every subset of A × B defines a function. For a set of ordered pairs to define a function, each input a ∈ A must appear exactly once. Other subsets of A × B may represent relations, but not necessarily functions.
Degree of a Function
The degree of an algebraic function is defined as the degree of the polynomial \( P(x,y) \) in the variables \( x \) and \( y \) that appears in its implicit equation \[ P(x,y)=0 \]
More precisely, determining the degree of an algebraic function amounts to identifying the highest total degree among the monomials of the polynomial \( P(x,y) \) that implicitly defines the function.
Example
Consider the function
\[ y=\sqrt{x^2+1} \]
To express this function in implicit form, the square root is removed by squaring both sides of the equation:
\[ y^2=x^2+1 \]
All terms are then collected on the left-hand side, yielding the implicit equation of the function:
\[ x^2 - y^2 + 1 = 0 \]
The corresponding polynomial is therefore:
\[ P(x,y)=x^2-y^2+1 \]
The degree of this polynomial is 2, since the terms of highest degree are \( x^2 \) and \( y^2 \), each of total degree 2.
Accordingly, the function \( y=\sqrt{x^2+1} \) is an algebraic function of degree 2.
A Concrete Example of a Function
Example 1
Consider the function f: ℝ → ℝ defined by:
$$ f(x) = x^2 + 1 $$
For every real number x, there is a corresponding value f(x):
$$ f(0) = 0^2 + 1 = 1 \\ f(1) = 1^2 + 1 = 2 \\ f(2) = 2^2 + 1 = 5 \\ \vdots $$
Example 2
A function may also map between sets of different types.
In this case, the domain is the set of real numbers, while the codomain is the set of integers:
$$ f: \mathbb{R} \rightarrow \mathbb{Z} $$
For example, consider the function f(x) = ⌊x⌋ (the floor function):
$$ f(2.2) = \lfloor 2.2 \rfloor = 2 \\ f(3.4) = \lfloor 3.4 \rfloor = 3 \\ f(3.5) = \lfloor 3.5 \rfloor = 3 \\ \vdots $$
Graph of a Function
Each input value a from the domain appears exactly once in the ordered pairs (a, b). The same output value b, however, may appear multiple times.
This allows us to represent the graph of the function f: A → B using a Cartesian diagram.
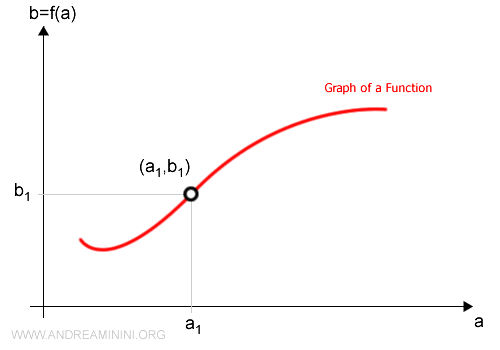
The horizontal axis (x-axis) corresponds to input values a ∈ A (the domain), and the vertical axis (y-axis) corresponds to output values b ∈ B (the codomain).
Each point in the diagram belongs to the Cartesian product A × B, but only the points on the red curve belong to the function’s graph.
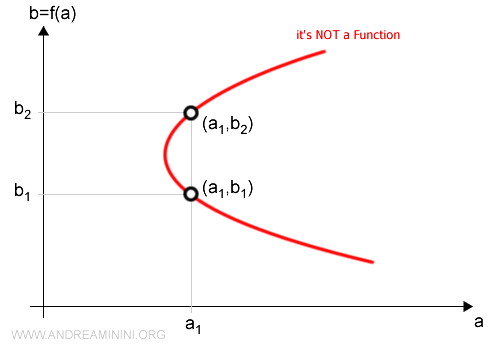
Note. This illustrates once again that the graph of a function is a subset of A × B. However, not every subset of A × B represents a function. For instance, the following graph is not valid, as some input values a appear more than once in the ordered pairs (a, b).
Positive and Negative Values of a Function
In intervals where the function satisfies y = f(x) > 0, it is said to be positive.
In intervals where y = f(x) < 0, the function is considered negative.
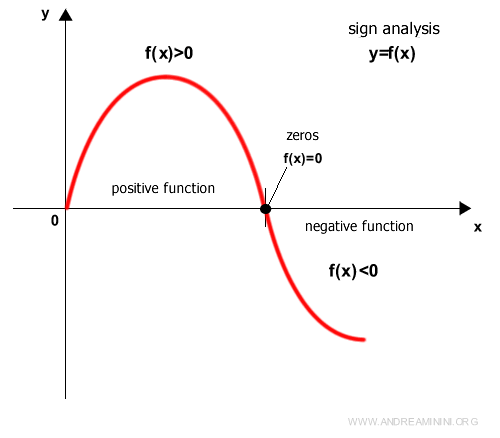
The points where f(x) = 0 are called the zeros of the function.
We determine the sign of a function using a sign analysis.
Note. Other features of a function - such as increasing/decreasing behavior, concavity, convexity, extrema, and inflection points - are analyzed through a more detailed study of the function using tools from calculus.
Classification of functions
Functions are classified according to the mathematical operations that appear in the expression f(x).
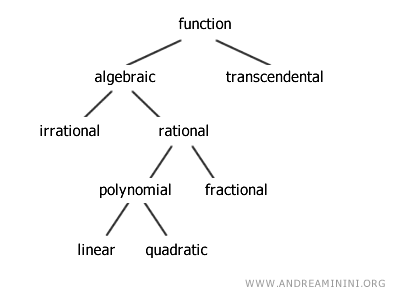
In particular, algebraic functions are those constructed using the four basic arithmetic operations (addition, subtraction, multiplication, and division), together with powers and or roots.
More broadly, functions that are not algebraic are referred to as transcendental functions. Typical examples are functions in which the independent variable x appears as the argument of a trigonometric function, a logarithmic function, or an exponential function.
Example. An example of an algebraic function is $$ y=2x^3-x $$ An example of a transcendental function is $$ y=2x^3- \sin(x) $$ The presence of even a single transcendental component is sufficient for the entire function to be classified as transcendental.
Algebraic functions are further divided into irrational and rational functions, depending on whether the variable x appears under a radical or only with integer exponents.
Example. An example of an irrational algebraic function is $$ y=2x^3-\sqrt{x} $$ An example of a rational algebraic function is $$ y=2x^3- x $$
Rational functions are then classified as polynomial or fractional, depending on whether the expression consists of a single polynomial or of the ratio of two polynomials.
Example. An example of a polynomial function is $$ y=2x^3-x $$ An example of a fractional rational function is $$ y= \frac{2x^3-2}{x^2+2x-5} $$
Polynomial functions are said to be linear if the polynomial has degree one in the variable x, and quadratic if it has degree two.
Example. An example of a linear function is $$ y=2x-1 $$ An example of a quadratic function is $$ y= 2x^2 -1 $$
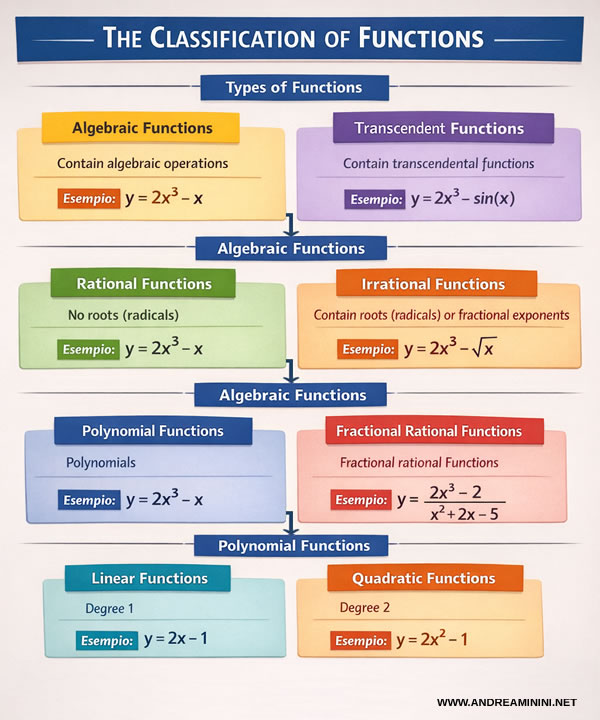
In summary, the diagram below provides an overview of the main types of functions and their classification.
Concave and Convex Functions
On a given interval [a, b], a function is described as:
- Convex
if its graph lies above the tangent line at every point on the curve.
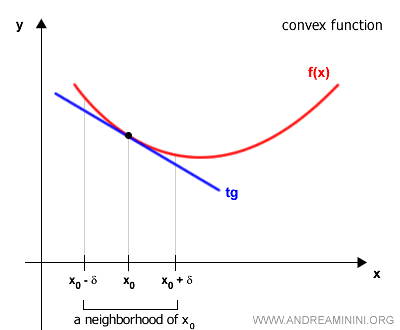
- Concave
if its graph lies below the tangent line at each point.
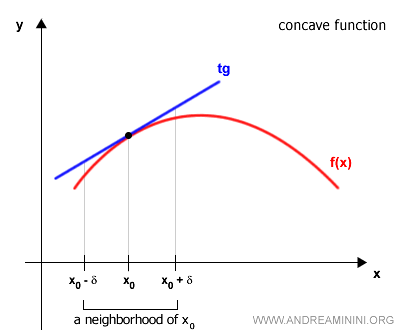
A function may be concave or convex throughout its entire domain or only over specific intervals.
Note. In addition to concave and convex functions, there are also constant functions that are neither concave nor convex.
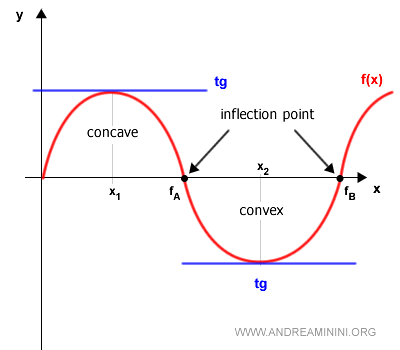
Furthermore, at certain critical points - known as points of inflection - a function may change concavity, being concave on one side and convex on the other (or vice versa).
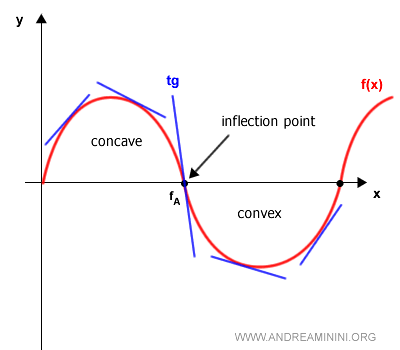
Image and Preimage
The image of a set A (the domain) under a function f is the corresponding set B (the codomain):
$$ B = f(A) $$
The preimage (or inverse image) of B under f is the original set A. It corresponds to the inverse relation f-1, which associates each element of B with one and only one element of A:
$$ A = f^{-1}(B) $$
Note. Every relation has an inverse relation. However, not all functions have an inverse function f-1. In many cases, the inverse relation does not define a function, because a single value in the codomain corresponds to multiple values in the domain. For example, the function f(x) = x2 does not have an inverse function, because y = 4 corresponds to both x = 2 and x = -2 in the domain of f.
Injective, Surjective, and Bijective Functions
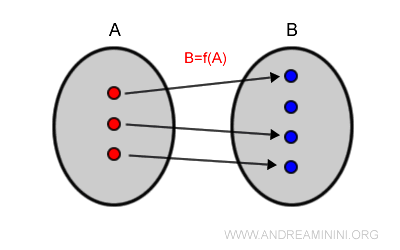
A function is injective (or one-to-one) if each element of the domain maps to a unique value in the codomain: $$ x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) $$
Example 1
The function y = x + 2 is injective, because no two distinct x-values produce the same output y.
For example, x = 2 and x = -2 map to y = 4 and y = 0, respectively.
Example 2
The function y = x2 is not injective, since distinct inputs can yield the same output: x = 2 and x = -2 both give y = 4.
A function is surjective (or onto) if every element of the codomain is the image of at least one element of the domain: $$ \forall \ b \in B, \:\: \exists \ a \in A \text{ such that } f(a) = b $$ 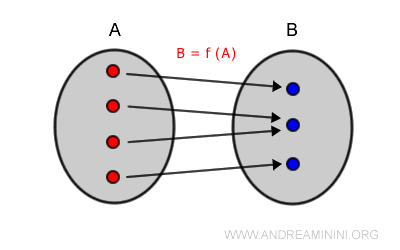
Example 1
The function y = x2 is not surjective when the codomain is ℝ, because negative numbers have no real square roots and thus no preimage.
Example 2
The function y = x + 1 is surjective over ℝ, since every real number y corresponds to some x = y - 1 in the domain.
A function is bijective (or one-to-one correspondence) if it is both injective and surjective.
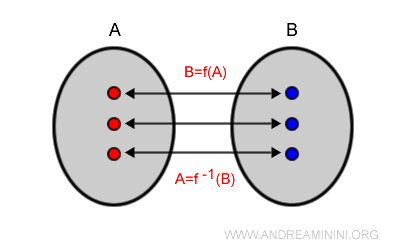
Only bijective functions y = f(x) always admit an inverse function x = f-1(y).
For a bijective function, the composition with its inverse returns the original input value. This is called the identity function:
$$ f^{-1}(f(x)) = x $$
Note. A function is called the identity function if it satisfies f(x) = x for all x in its domain.
Composite Functions
Given two functions f: A → B and g: B → C, the composition of f with g is denoted as: $$ f \circ g : A \rightarrow C $$ or equivalently: $$ F = f[g(x)] $$ Here, f is the outer function, and g is the inner function.
Example
Let f(x) and g(x) be defined as follows:
$$ f(x) = x + 1 $$
$$ g(x) = 2x + 3 $$
The composite function g ∘ f is:
$$ g(f(x)) = g(x + 1) = 2(x + 1) + 3 = 2x + 5 $$
And so on.
