Sinusoidal Functions

Sinusoidal functions (or sinusoid ∿) are based on the sine or cosine functions. $$ y = A \cdot \sin(\omega x + \phi) $$ $$ y = A \cdot \cos(\omega x + \phi) $$ where A is the amplitude, ω (omega) is the angular frequency (radians per second), and φ (phi) is the phase shift. $$ A, \omega, \phi \in R $$

The two formulas are equivalent because cosine is essentially a sine wave shifted by π/2 (90°).

$$ y = A \cdot \cos(\omega x + \phi) = A \cdot \sin(\omega x + \phi + \frac{\pi}{2}) $$

Visually, the difference between sine and cosine waves becomes clear.

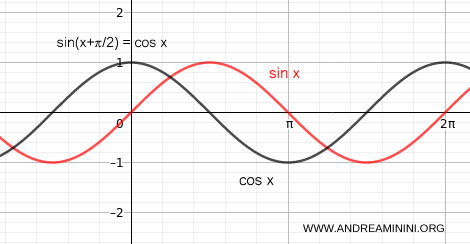
Conversely, sine can be seen as a cosine wave shifted by -π/2 (-90°).

$$ y = A \cdot \sin(\omega x + \phi) = A \cdot \cos(\omega x + \phi - \frac{\pi}{2}) $$

Another way to express the relationship between sine and cosine is:

$$ \sin x = \cos(x - \frac{\pi}{2}) = \cos(\frac{\pi}{2} - x) $$

$$ \cos x = \sin(x + \frac{\pi}{2}) = \sin(\frac{\pi}{2} - x) $$

As a result, any sinusoid can be expressed either as a sine or cosine wave, depending on which simplifies the calculation.

Note: Whether you use sine or cosine depends on the situation. Often, choosing one over the other makes an algebraic expression simpler.

What are sinusoidal waves used for?

Sinusoids are essential in describing many physical phenomena.

For example, in physics, they are used to model circular motion, simple harmonic motion, alternating current, or a sinusoidal signal in telecommunications.

Note: Through Fourier analysis, any complex periodic signal can be decomposed into a sum of sinusoidal waves.

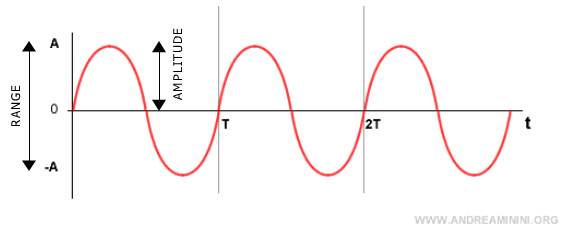
Amplitude

The amplitude |A| of a sinusoid determines the height of the wave and its range, from -A to A.

Angular Frequency (or Pulsation)

Angular frequency (or pulsation) measures how many radians the wave covers per second and is related to the period T of the sinusoid.

$$ \omega = \frac{2 \pi}{T} $$

Since frequency f is the inverse of the period T:

$$ f = \frac{1}{T} $$

we can also express the angular frequency ω as:

$$ \omega = 2 \pi f $$

The more radians or cycles a sinusoid completes in a second, the higher its angular frequency ω (in rad/s).

Note: The denominator 2π represents the radians in a full circle, or 360°.

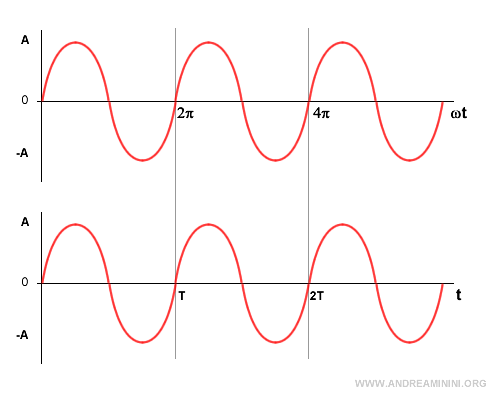
The argument of the sinusoidal function ωt equals 2π when t = 1.

$$ \omega t = 2 \pi $$

This relationship is illustrated in the following graphs, where ωt = 2π is clearly visible.

If we increase the angular frequency, the function completes more cycles (radians) in a second.

For instance, let’s compare two sinusoidal waves:

The red wave completes ω = 2 cycles per second, while the blue wave completes ω = 4 cycles per second.

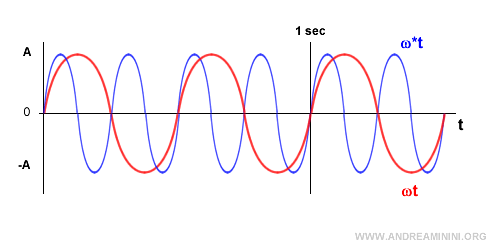
As a result, the blue wave has a higher angular frequency than the red wave (ω*>ω). In one second, the blue wave covers more radians.

In this example, the blue wave’s angular frequency is twice that of the red wave (ω* = 2ω).

Therefore, changing the angular frequency ω affects the period T of the sinusoid.

$$ T = \frac{2 \pi}{\omega} $$

Period

A sinusoid is periodic, meaning it repeats at regular intervals. $$ y(t) = y(t + T) $$

For example, at times t₁ and t₁ + T, the sinusoidal wave takes the same value, y(t₁) = y(t₁ + T) = -A.

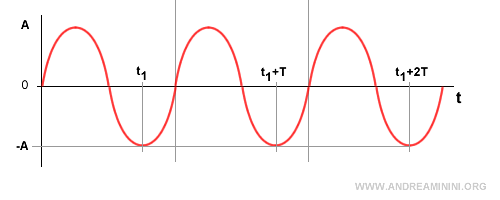
This holds for any multiple of T, meaning y(t₁) = y(t₁ + kT) = -A where k = 1, 2, 3, and so on.

$$ y(t) = y(t + kT) \ \ \ \ k=1,2,3,... $$

In general, considering the angular frequency ω and phase shift φ, the periodic formula of a sinusoid can be written as:

$$ y = \sin(x + kT) $$

$$ y = \sin (\omega (x + kT) + \phi) $$

Any change in the angular frequency ω modifies the period.

Since T = 2π/ω, increasing the angular frequency (Δω>0) shortens the period T.

$$ T = \frac{2 \pi}{\omega} $$

Conversely, decreasing the angular frequency (Δω<0) lengthens the period T.

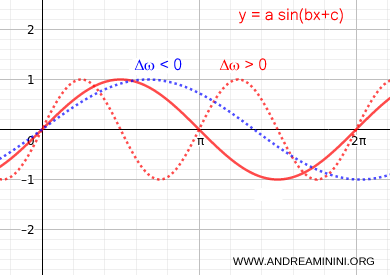
Note: Changing the phase shift doesn’t affect the period T of the sinusoid.

Stretching and Compressing Sinusoids

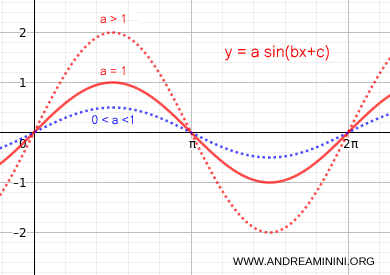
Any sinusoid can be generalized using this formula: $$ y = a \sin (b \cdot x + c) $$

• The coefficient a causes a vertical stretch (a>1) or vertical compression (0<a<1) of the wave’s amplitude.
  
• The coefficient b causes a horizontal stretch (0<b<1) or horizontal compression (b>1) of the wave. Changing b (the angular frequency ω) alters the period (T) of the sinusoid.
  

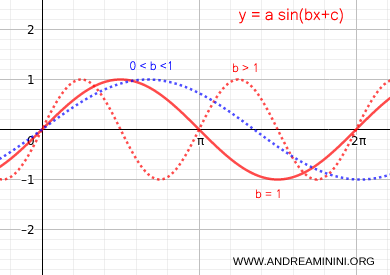
  Note: In practice, if b>1, the angular frequency increases , and the wave completes more radians per second (more oscillations). If 0<b<1, the angular frequency decreases, resulting in fewer oscillations per second.

• The coefficient c causes a horizontal shift, moving the wave backward (c>0) or forward (c<0). This shift is known as the phase shift.
  

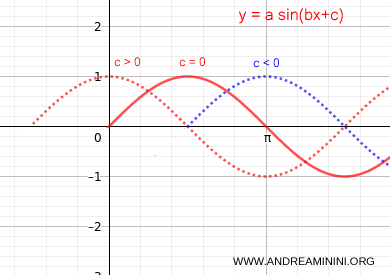
  Note: In signal theory, shifting the wave backward (c>0) is referred to as an advance, meaning the sinusoid starts before time zero. Shifting it forward (c<0) is called a delay, meaning the sinusoid starts after time zero.

And so on.