Sine Function in Trigonometry
In the unit circle, the trigonometric function sine associates the measure of an angle α with a vertical segment. It is commonly denoted as sin(α) or sen(α) in Italian texts, and it can take values between -1 and +1.
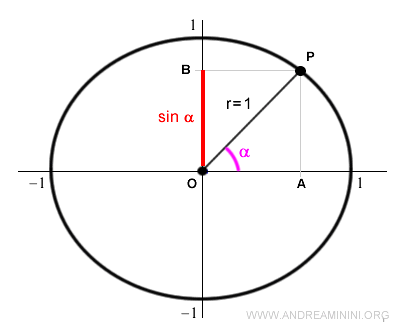
The angle α determines a point P on the unit circle.
The projection of point P onto the vertical axis gives the length of the segment OB, known as the sine of α.
Note: The sine can be measured equally by either segment OB or segment AP, as $$ \overline{OB} = \overline{AP} $$
In general, the sine of an angle α is the ratio of the side opposite the angle to the hypotenuse in a right triangle.
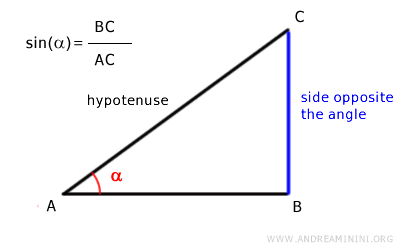
The maximum length of this segment is equal to the radius of the unit circle.
Since the unit circle has a radius of 1 (r = 1), the sine function's values are restricted to the range between -1 and +1.
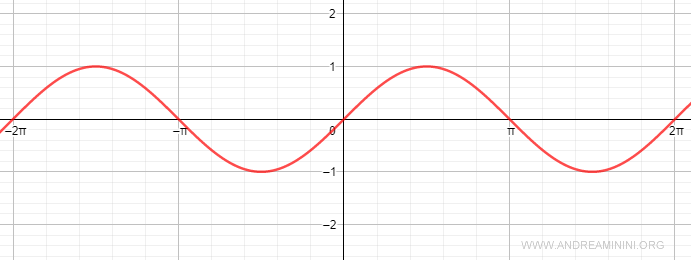
As a result, the sine function's range is [-1, 1].
$$ -1 \leq \sin \alpha \leq 1 $$
Here are some key angles and their sine values:
| Angle (Degrees) | Angle (Radians) | Sine |
|---|---|---|
| $$ 0° $$ | $$ 0 $$ | $$ 0 $$ |
| $$ 30° $$ | $$ \frac{\pi}{6} $$ | $$ \frac{1}{2} $$ |
| $$ 45° $$ | $$ \frac{\pi}{4} $$ | $$ \frac{\sqrt{2}}{2} $$ |
| $$ 60° $$ | $$ \frac{\pi}{3} $$ | $$ \frac{\sqrt{3}}{2} $$ |
| $$ 90° $$ | $$ \frac{\pi}{2} $$ | $$ 1 $$ |
| $$ 180° $$ | $$ \pi $$ | $$ 0 $$ |
| $$ 270° $$ | $$ \frac{3 \pi}{2} $$ | $$ -1 $$ |
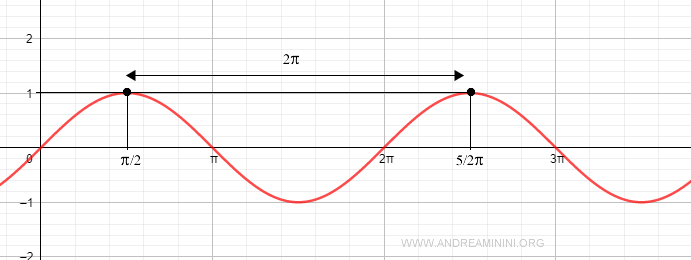
Sine is a periodic function with a period of 2π.
Here, 2π represents a full rotation around the unit circle, or an angle of 360°.
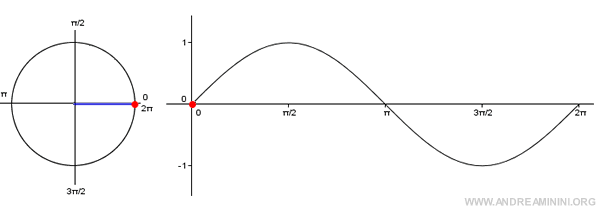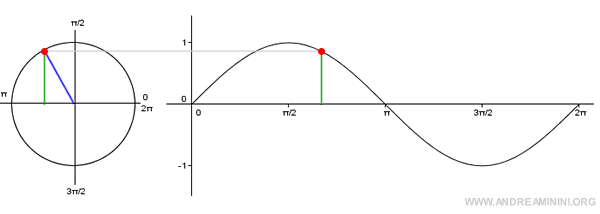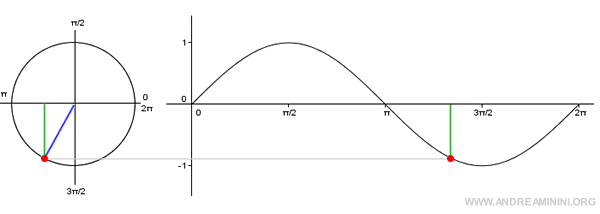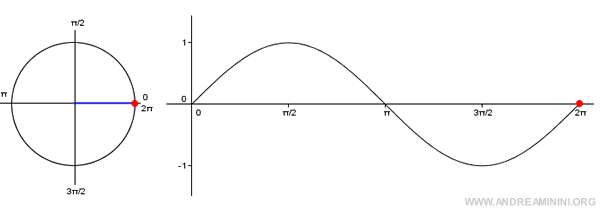
Note: The graph of the sine function is known as a sinusoid. It is created by plotting the angles on the x-axis and their corresponding sine values on the y-axis. Since sine is a periodic function, it’s enough to consider angles within the interval [0, 2π].
When you add one or more full rotations (2π) to a given angle α, you still reach the same point P on the unit circle, and the sine function will return the same value.
$$ \sin \alpha = \sin ( \alpha + n \cdot 2 \pi ) $$
For instance, both sin(π/2) and sin(π/2 + 2π) yield the value one.
Note: From a mathematical standpoint, the sine function is also an odd function because $$ \sin(- \alpha) = - \sin \alpha $$ The sine of an oriented angle α and its opposite -α have the same absolute value, but opposite signs.
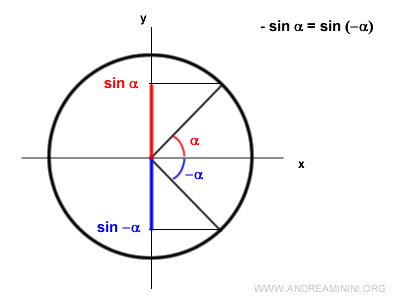
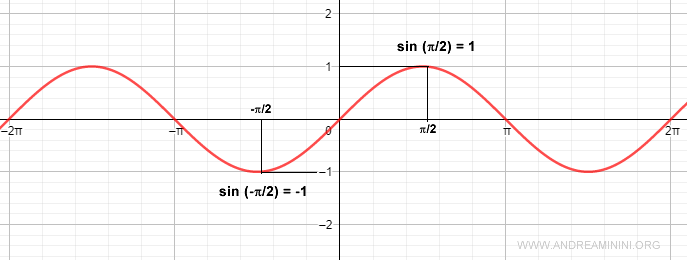
For example, the sine of π/2 is +1, while the sine of -π/2 is -1.
The Origin of the Word "Sine"
The word "sine" comes from the Indian term jiiva, used by the mathematician and astronomer Aryabhata in the 5th century AD to refer to half-chords of a circle.
This term was later translated into Arabic as jaib, meaning "fold" or "pocket."
In Europe, the Arabic word "jaib" was then translated into Latin as sinus, meaning "curve" or "fold," which eventually gave rise to the term "sine."
