Radians
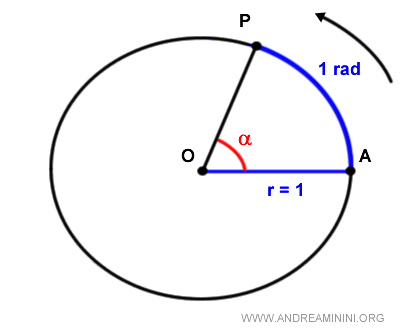
In a unit circle, a radian is the angle subtended by an arc whose length is equal to the radius.
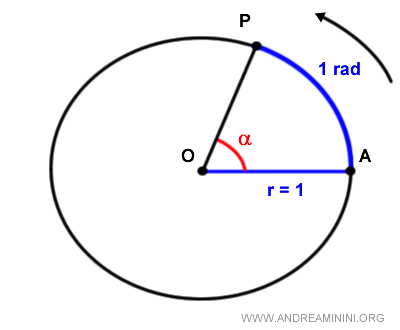
One radian is approximately 57.3° in the degree system.
Radians are the unit of measurement for angles.
They are denoted by the symbol rad.
Note: There are other units for measuring angles. Unless otherwise specified, it is assumed that the measurement is in radians even if the rad symbol is omitted.
Proof
Consider the same angle α in two circles with different radii, r and r'.
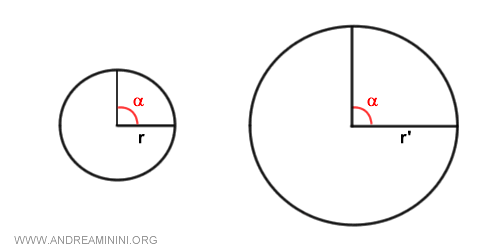
If I measured the size of the angles by the length of the arc, I would get two different lengths.
For the same angle, the second circle has a longer arc (k'>k) than the first circle.
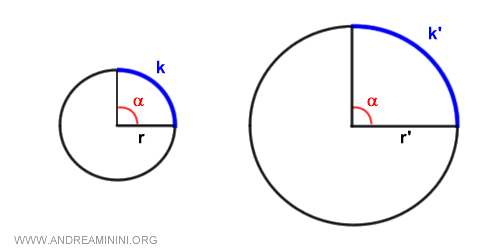
According to the proportionality between angles and arcs:
$$ k : \alpha = 2 \pi r : 360° $$
$$ k' : \alpha = 2 \pi r' : 360° $$
This means:
$$ \frac{k}{\alpha} = \frac{2 \pi r}{360°} $$
$$ \frac{k'}{\alpha} = \frac{2 \pi r'}{360°} $$
Highlighting the arc lengths:
$$ k = \frac{2 \pi r \cdot \alpha}{360°} $$
$$ k' = \frac{2 \pi r' \cdot \alpha}{360°} $$
Simplifying 2 and 360:
$$ k = \frac{\pi r \alpha}{180°} $$
$$ k' = \frac{\pi r' \alpha}{180°} $$
Dividing both sides:
$$ \frac{k}{k'} = \frac{\frac{\pi r \alpha}{180°}}{\frac{\pi r' \alpha}{180°}} $$
$$ \frac{k}{k'} = \frac{\pi r \alpha}{180°} \cdot \frac{180°}{\pi r' \alpha} $$
$$ \frac{k}{k'} = \frac{r}{r'} $$
By moving the quantities of the first circle to the left and those of the second circle to the right:
$$ \frac{k}{r} = \frac{k'}{r'} $$
We notice that the ratio between the length of the arc and the radius is the same in both circles.
$$ k : r = k' : r' $$
This means the ratio between the arc and the radius (k/r) does not change with the size of the circle.
Therefore, the k/r ratio is a reliable unit of measurement for the size of an angle because it is universal and allows for comparison of angles from circles with different radii.
$$ \alpha = \frac{k}{r} $$
The k/r ratio is called the radian (rad) and is equal to 1 when the length of the arc k is equal to the length of the radius r.
The Measurement of Key Angles in Radians and Degrees
This table summarizes the key angle measurements in radians and degrees:
| Degrees | Radians |
|---|---|
| 0° | 0 |
| 15° | π/12 |
| 30° | π/6 |
| 45° | π/4 |
| 60° | π/3 |
| 90° | π/2 |
| 120° | 2/3 π |
| 135° | 3/4 π |
| 150° | 5/6 π |
| 180° | π |
| 270° | 3/2 π |
| 360° | 2 π |
How to Remember Them All? Initially, this can be challenging. However, if you remember that $$ 15° = \frac{\pi}{12} \ rad $$ you can reconstruct all the others: $$ 30° = 2 \cdot 15° = 2 \cdot \frac{\pi}{12} = \frac{\pi}{6} \ rad $$ $$ 45° = 3 \cdot 15° = 3 \cdot \frac{\pi}{12} = \frac{\pi}{4} \ rad $$ $$ 60° = 4 \cdot 15° = 4 \cdot \frac{\pi}{12} = \frac{\pi}{3} \ rad $$ $$ 90° = 6 \cdot 15° = 6 \cdot \frac{\pi}{12} = \frac{\pi}{2} \ rad $$ Alternatively, for more precise calculations, remember that 1° equals $$ 1° = \frac{2\pi}{360} = \frac{\pi}{180} \ rad $$ And so on.
Why is a Full Circle 2π Radians?
Consider the entire circumference, a full circle, which is a 360° angle.
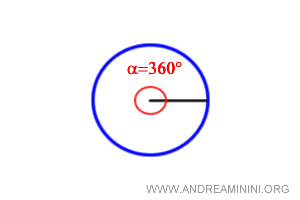
From geometry, we know that the length of a circumference is equal to the radius r multiplied by 2 pi (π).
$$ k = 2 \pi r $$
Knowing the length of the circumference (k) and the radius (r), we can calculate the angle in radians (rad) as:
$$ \alpha = \frac{k}{r} \ rad $$
Substituting k with 2πr, we get:
$$ \alpha = \frac{2 \pi r}{r} \ rad $$
Simplifying, we find the measure of the circumference in radians:
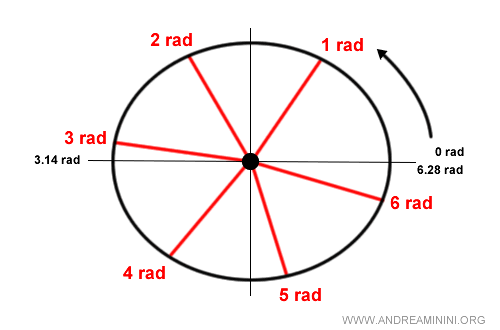
$$ \alpha = 2 \pi \ rad $$
Knowing that pi (π) equals 3.14:
$$ \alpha = 2 \cdot 3.14 \ rad = 6.28 \ rad $$
In conclusion, a full circle (360°) measures 2π radians, or 6.28 radians.
Note: If a full circle (360°) equals 2π radians, a straight angle (180°) is π radians, or 3.14 radians, since it is exactly half. Therefore, a right angle (90°) is π/2 radians. And so on.
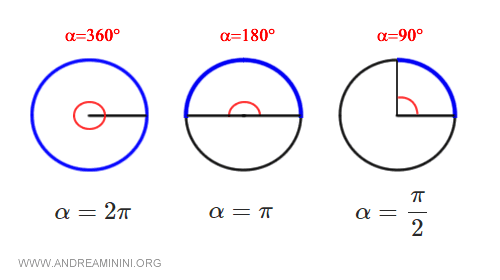
And so forth.
