Arctangent

What is the arctangent?

In trigonometry, the arctangent is the inverse of the tangent function. It's often written as arctg, arctan, tg^-1, or tan^-1. $$ y = arctan \ x $$

Here, x represents the value of the tangent.

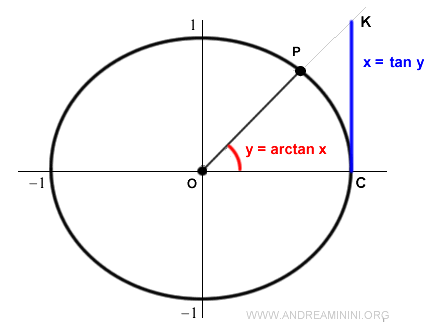
The arctangent function returns the angle y corresponding to the given tangent value.

$$ y = \ arctan \ x $$

Where x is the tangent value

$$ x = \tan y $$

The graph of the arctangent looks like this:

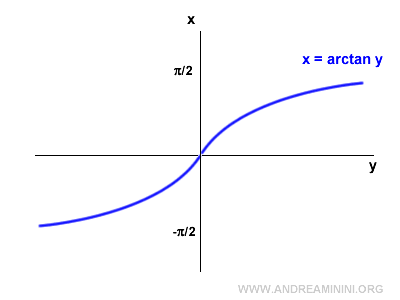
Note: The domain of the arctangent is all real numbers because it aligns with the range of the tangent function. $$ D_{arctan} = ( -\infty ; +\infty ) $$ Its range, however, is the interval [-π/2, π/2].

A Practical Example

The tangent of π/4 is 1.

$$ \tan \frac{\pi}{4} = 1 $$

Since the arctangent is the inverse of the tangent function,

the arctangent of 1 is π/4.

$$ \arctan 1 = \frac{\pi}{4} $$

Note: The arctangent of the tangent returns the angle itself. $$ \arctan (\tan \frac{\pi}{4} )= \frac{\pi}{4} $$

How to Draw the Arctangent Graph

Let's start with the tangent graph.

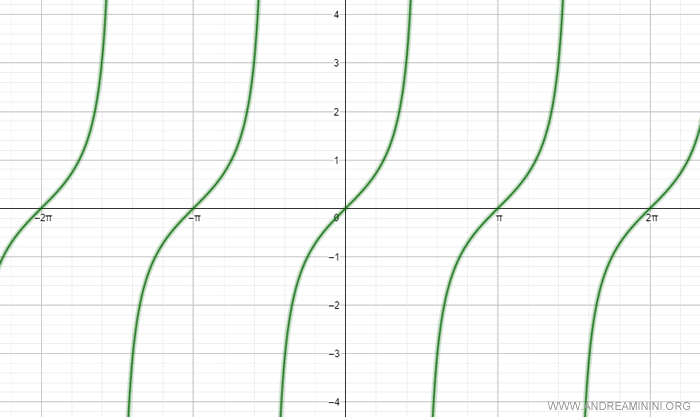
The tangent function is not invertible because it is not a one-to-one (bijective) function.

To make it one-to-one, we limit the domain to the interval [-π/2, π/2].

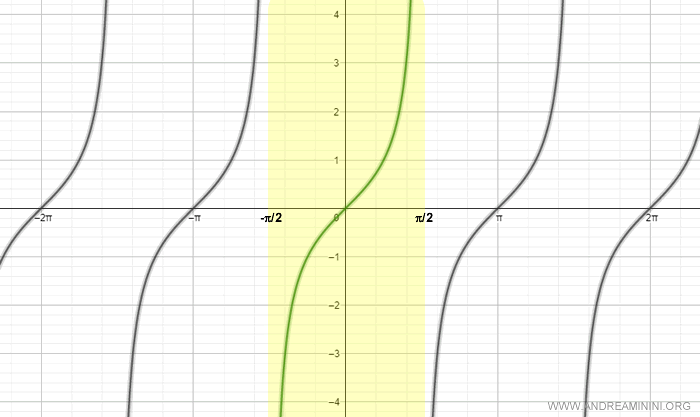
Within this interval, the tangent is a bijective function and therefore invertible.

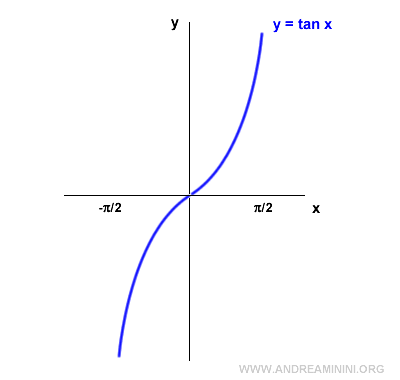
Next, rotate the graph 90° counterclockwise.

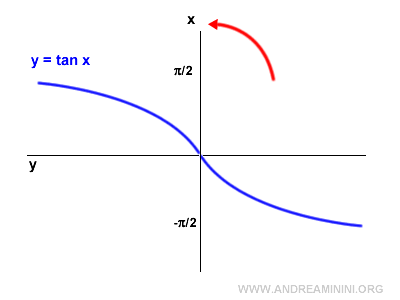
Then, flip the graph horizontally by reflecting it across the vertical axis.

The result is the graph of the arctangent.

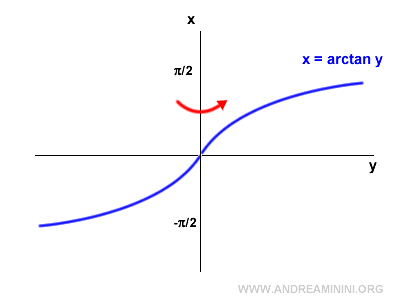
The arctangent is also an invertible function.

Its inverse is the tangent function, restricted to the interval [-π/2, π/2].

Note: The tangent can be made invertible over other intervals where it is bijective, such as [π/2, 3π/2]. In such cases, the arctangent value falls within that chosen interval.

And so on.