Law of Sines
In any triangle, the sides are proportional to the sines of their opposite angles: $$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{BC}}{\sin \alpha} = \frac{\overline{AC}}{\sin \beta} $$
Here, α, β, and γ represent the angles opposite sides BC, AC, and AB, respectively.
This theorem is also known as Euler's Law of Sines.
A Practical Example
Let’s solve a triangle
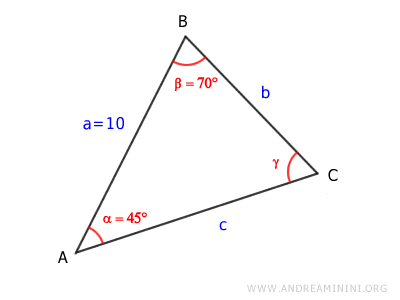
where we know two angles and the length of one side.
$$ \alpha = 45° $$
$$ \beta = 70° $$
$$ \overline{AB} = 10 $$
First, let's find the missing angle.
Since the angles of a triangle add up to 180°, we can calculate γ by subtracting α and β.
$$ \alpha + \beta + \gamma = 180° $$
$$ \gamma = 180° - \alpha - \beta $$
$$ \gamma = 180° - 45° - 70° $$
$$ \gamma = 65° $$
Now we have all three angles of the triangle.
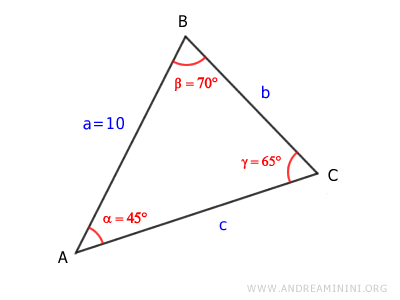
With the angles known, we can use the Law of Sines to calculate the remaining side lengths.
$$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{BC}}{\sin \alpha} = \frac{\overline{AC}}{\sin \beta} $$
$$ \frac{\overline{AB}}{\sin 65°} = \frac{\overline{BC}}{\sin 45°} = \frac{\overline{AC}}{\sin 70°} $$
We already know that AB is 10, so
$$ \frac{10}{\sin 65°} = \frac{\overline{BC}}{\sin 45°} = \frac{\overline{AC}}{\sin 70°} $$
Now, let's compare the first and second parts to find the length of BC.
$$ \frac{10}{\sin 65°} = \frac{\overline{BC}}{\sin 45°} $$
$$ \overline{BC} = \frac{10}{\sin 65°} \cdot \sin 45° $$
$$ \overline{BC} = 7.8 $$
Next, we compare the first and third parts to find the length of AC.
$$ \frac{10}{\sin 65°} = \frac{\overline{AC}}{\sin 70°} $$
$$ \overline{AC} = \frac{10}{\sin 65°} \cdot \sin 70° $$
$$ \overline{AC} =10.37 $$
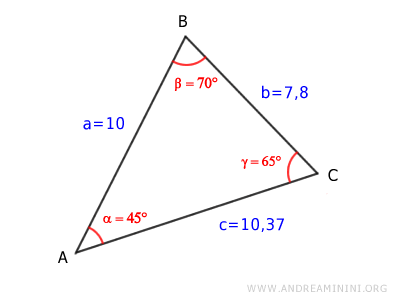
So, the side lengths of the triangle are:
$$ \overline{AB} = 10 $$
$$ \overline{BC} = 7.8 $$
$$ \overline{AC} = 10.37 $$
We’ve now solved the triangle.
The Proof
Consider any triangle inscribed in a circle with radius r.
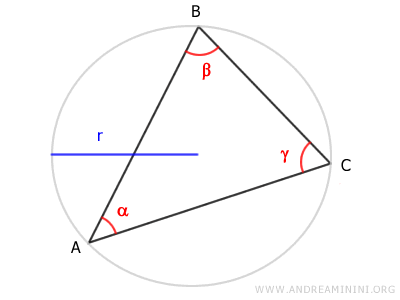
According to the Chord Theorem, each side of the triangle equals the product of the circle’s diameter (2r) and the sine of the opposite angle.
$$ \overline{AB} = 2r \cdot \sin \gamma $$
$$ \overline{AC} = 2r \cdot \sin \beta $$
$$ \overline{BC} = 2r \cdot \sin \alpha $$
Highlighting the diameter (2r) in each relation, we get
$$ \frac{ \overline{AB} }{ \sin \gamma } = 2r $$
$$ \frac{ \overline{AC} }{ \sin \beta } = 2r $$
$$ \frac{ \overline{BC} }{ \sin \alpha } = 2r $$
Each ratio equals the diameter 2r.
This establishes the following equality:
$$ \frac{ \overline{AB} }{ \sin \gamma } = \frac{ \overline{AC} }{ \sin \beta } = \frac{ \overline{BC} }{ \sin \alpha } = 2r $$
This shows that the sides of the triangle are proportional to the sines of their opposite angles:
$$ \frac{ \overline{AB} }{ \sin \gamma } = \frac{ \overline{AC} }{ \sin \beta } = \frac{ \overline{BC} }{ \sin \alpha } $$
And thus, the Law of Sines is proven.
And so on.
