A Simple Method to Memorize Sine, Cosine, and Tangent for Angles 0°, 30°, 45°, 60°, and 90°
This method uses the fingers of one hand to easily remember the sine, cosine, and tangent values for the angles 0°, 30°, 45°, 60°, and 90°.
The trick is to count the number of fingers to the left and right of the finger representing a specific angle.
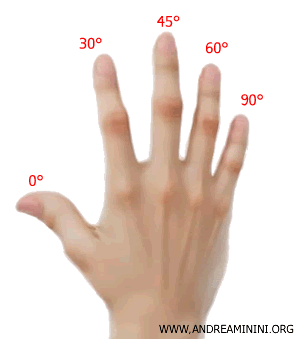
Each finger on your right hand corresponds to an angle $ \alpha $:
- Thumb: 0°
- Index finger: 30°
- Middle finger: 45°
- Ring finger: 60°
- Pinky finger: 90°
To calculate the cosine, sine, and tangent of an angle $ \alpha $, look at the finger associated with the angle and apply these formulas:
- Cosine of the angle
The cosine of an angle $ \alpha $ is the square root of the number of fingers to the right of the finger representing the angle, divided by 2: $$ \cos( \alpha ) = \frac{ \sqrt{ \text{number of fingers on the right} } }{2} $$ - Sine of the angle
The sine of an angle is the square root of the number of fingers to the left of the finger representing the angle, divided by 2: $$ \sin( \alpha ) = \frac{ \sqrt{ \text{number of fingers on the left} } }{2} $$ - Tangent of the angle
The tangent of $ \alpha $ is simply the sine divided by the cosine: $$ \tan{\alpha} = \frac{ \sin{ \alpha } }{ \cos{ \alpha }} $$
With this method, you can quickly find the trigonometric values of these angles using just one hand.
Note: If you want to use your left hand instead, simply reverse the sine and cosine formulas. I use the right hand because it's easier to remember.
A Practical Example
Let’s calculate the cosine, sine, and tangent of 60°.
The 60° angle corresponds to the ring finger on your right hand.
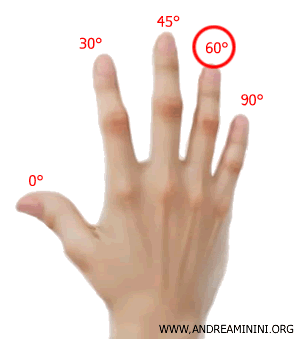
There’s only one finger (the pinky) to the right of the ring finger, so the cosine of 60° is:
$$ \cos( 60° ) = \frac{ \sqrt{ \text{num. of fingers on the right} } }{2} = \frac{ \sqrt{1} }{2} = \frac{1}{2} $$
There are three fingers to the left of the ring finger, so the sine of 60° is:
$$ \sin( 60° ) = \frac{ \sqrt{ \text{num. of fingers on the left} } }{2} = \frac{ \sqrt{3} }{2} $$
Finally, with the sine and cosine values known, we can calculate the tangent of 60° using the formula $ \tan(a)=\sin(a)/\cos(a) $:
$$ \tan(60°) = \frac{\sin(60°)}{\cos(60°)} = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} = \sqrt{3} $$
All the values check out.
| Angle | Sine | Cosine | Tangent | |
|---|---|---|---|---|
| Radians | Degrees | |||
| 0 | 0° | 0 | 1 | 0 |
| π/6 | 30° | 1/2 | √3/2 | √3/3 |
| π/4 | 45° | √2/2 | √2/2 | 1 |
| π/3 | 60° | √3/2 | 1/2 | √3 |
| π/2 | 90° | 1 | 0 | ∞ |
And so on.
