Arccosine Function
What is Arccosine?
Arccosine is the inverse trigonometric function of the cosine within the interval [0, π]. It is commonly denoted by the symbol arccos.
Sometimes, arccosine is also written as cos-1, where the -1 is not an exponent but rather the mathematical symbol indicating the inverse function.
How Does Arccosine Work?
Given the cosine value y, arccosine calculates the angle x in radians that produces this value.
Example
The cosine of an angle is 0.5.
$$ cos \ \alpha \ = 0.5 $$
Which angle α results in this cosine value?
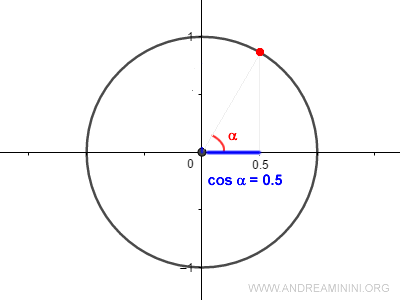
To find out, we use the arccosine of the cosine.
$$ \alpha = arccos (0.5) = \frac{ \pi }{ 3 } \ rad $$
Arccosine identifies the arc length x on the unit circle that corresponds to the given cosine value.
The arc is measured in radians and has the same magnitude as the angle x that defines the cosine.
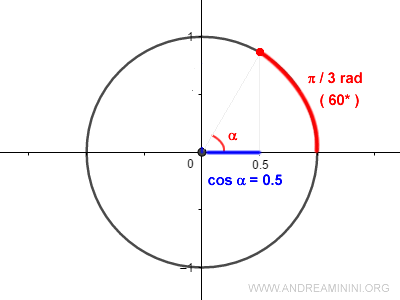
In this example, the cosine function equals 0.5 when the angle x is π/3 radians (60°).
The Explanation
The cosine function takes on values between -1 and +1.
As a periodic function, the same value of cos(x) can be achieved with multiple x values, or angles. For example, x1 and x2.
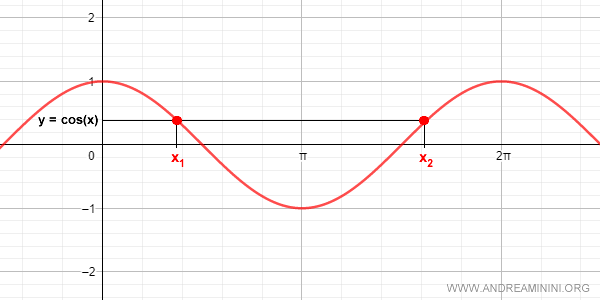
This makes it impossible to construct a unique inverse function for cosine over its entire domain because it would violate the one-to-one correspondence required for an inverse function.
$$ f:x -> y $$
How Do We Construct the Inverse of the Cosine Function?
There is a way to solve this problem.
By considering only a specific part of the cosine function's domain, we can ensure a one-to-one correspondence between x and y.
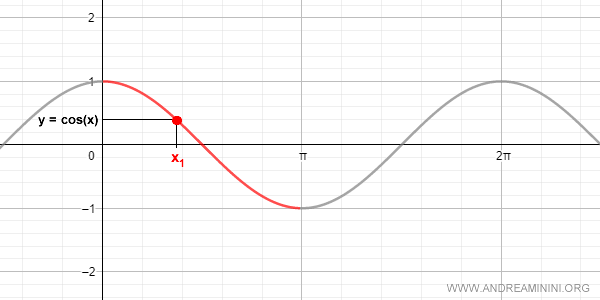
In the interval [0, π], there is a unique one-to-one relationship between the cosine values [-1, +1] and the variable x.
This is why we can construct the inverse of the cosine function in this interval.
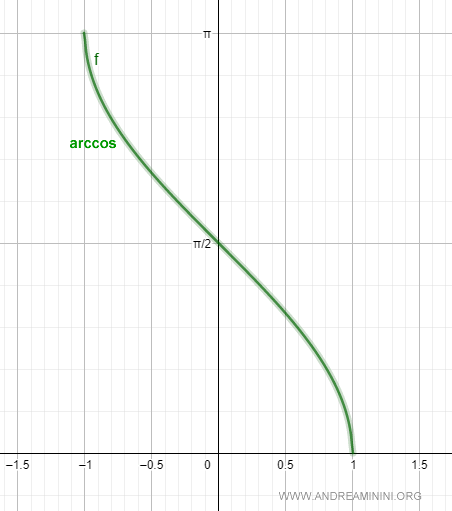
This inverse function is called arccosine.
$$ arccos(x) : [-1,1] → [0,π] $$
The arccosine is often written as arccos or acos.
Starting with a given cosine value, the arccosine function calculates the angle x that produces it within the interval [0, π].
Note: The interval [0, π] is not the only range where the cosine function is invertible. For example, we can also invert the cosine function in the interval [π, 2π] and in many other intervals where the cosine is bijective.
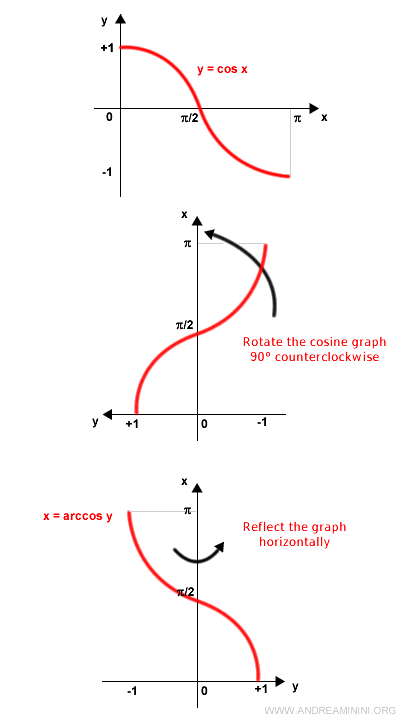
How to Construct the Graph of the Arccosine Function
The graph of the arccosine can be derived from the cosine graph over the restricted domain [0, π] through two simple steps:
- Rotate the cosine graph 90° counterclockwise.
- Reflect the graph horizontally.
The resulting graph is that of the arccosine.
Using the same logic, you can construct the graph of the arccosine from other reduced domains.
For instance, [-π, 0] or other intervals where the cosine is invertible.
And so on.
