Cosine Theorem

In any triangle, the square of one side, b², is equal to the sum of the squares of the other two sides, a² + c², minus twice the product of those two sides, 2ac, times the cosine of the angle α between them. $$ b^2 = a^2 + c^2 - 2ac \cdot \cos \alpha $$

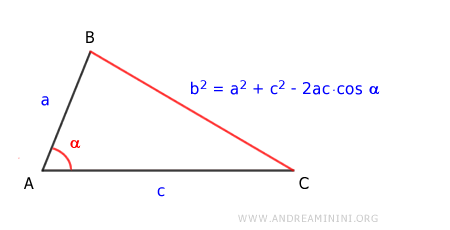
This theorem is also known as Carnot's Cosine Theorem.

Example

Let’s find the length of side BC in this triangle.

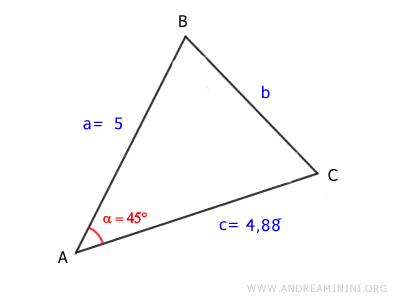
We know the lengths of sides AB and AC and the measure of angle α.

$$ \overline{AB} = 5 $$

$$ \overline{AC} = 4.88 $$

$$ \alpha = 45° $$

Using the cosine theorem, we can calculate the length of BC:

$$ \overline{BC}^2 = \overline{AB}^2 + \overline{AC}^2 - 2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha $$

Substituting AB = 5, AC = 4.88, and α = 45°:

$$ \overline{BC}^2 = 5^2 + (4.88)^2 - 2 \cdot (5 \cdot 4.88) \cdot \cos 45° $$

$$ \overline{BC}^2 = 14.3 $$

Now, taking the square root of both sides:

$$ \sqrt{\overline{BC}^2} = \sqrt{14.3} $$

$$ \overline{BC} = \sqrt{14.3} $$

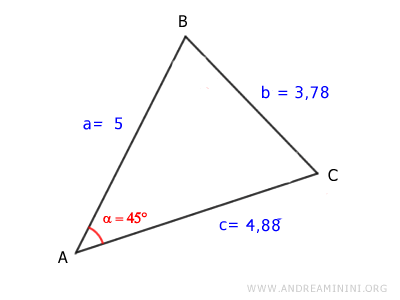
$$ \overline{BC} = 3.78 $$

Therefore, the length of side BC is 3.78.

 

The Proof

Let’s take a closer look at any triangle ABC.

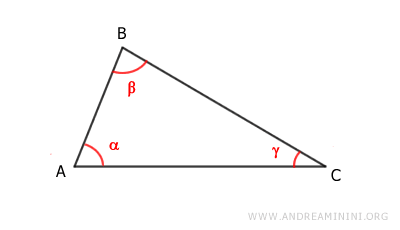
Draw the height h from A, creating two right triangles, ABD and BCD.

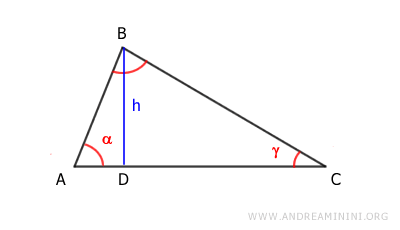
According to the first right triangle theorem, a leg of a right triangle is equal to the hypotenuse times the cosine of the adjacent angle or the sine of the opposite angle.

This gives us the lengths of BD and AD:

$$ \overline{BD} = \overline{AB} \cdot \sin \alpha $$

$$ \overline{AD} = \overline{AB} \cdot \cos \alpha $$

Here, AB is the hypotenuse of right triangle ABD, while BD and AD are the legs.

Since segment AC is the sum of segments AD and CD:

$$ \overline{AC} = \overline{AD} + \overline{CD} $$

we can find CD, the leg of triangle BCD, as follows:

$$ \overline{CD} = \overline{AC} - \overline{AD} $$

$$ \overline{CD} = \overline{AC} - \overline{AB} \cdot \cos \alpha $$

Applying the Pythagorean theorem, the square of the hypotenuse BC is equal to the sum of the squares of the legs in right triangle BCD:

$$ \overline{BC}^2 = \overline{BD}^2 + \overline{CD}^2 $$

Since CD = AC - AB · cos α,

$$ \overline{BC}^2 = \overline{BD}^2 + (\overline{AC} - \overline{AB} \cdot \cos \alpha )^2 $$

and BD = AB · sin α,

$$ \overline{BC}^2 = (\overline{AB} \cdot \sin \alpha)^2 + (\overline{AC} - \overline{AB} \cdot \cos \alpha )^2 $$

$$ \overline{BC}^2 = \overline{AB}^2 \cdot \sin^2 \alpha + \overline{AC}^2 - 2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha + \overline{AB}^2 \cdot \cos^2 \alpha $$

$$ \overline{BC}^2 = \overline{AB}^2 \cdot ( \sin^2 \alpha + \cos^2 \alpha) + \overline{AC}^2 - 2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha $$

By the fundamental trigonometric identity sin² α + cos² α = 1,

$$ \overline{BC}^2 = \overline{AB}^2 \cdot (1) + \overline{AC}^2 - 2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha $$

$$ \overline{BC}^2 = \overline{AB}^2 + \overline{AC}^2 - 2 \overline{AC} \cdot \overline{AB} \cdot \cos \alpha $$

This is the formula we aimed to prove.

or

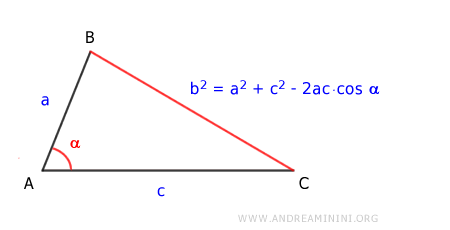
Note: When the triangle is a right triangle, the cosine theorem simplifies to the Pythagorean theorem, since in a right triangle, angle α is 90°, and the cosine of 90° is zero. $$ a^2 = b^2 + c^2 - 2bc \cdot \cos \alpha $$ $$ a^2 = b^2 + c^2 - 2bc \cdot \cos 90° $$ $$ a^2 = b^2 + c^2 - 2bc \cdot 0 $$ $$ a^2 = b^2 + c^2 $$

And so forth.