Cosine Function in Trigonometry
In the unit circle, the trigonometric function cosine links the size of an angle α to a segment along the horizontal axis. It's denoted as cos(α) and its value always falls between -1 and +1.
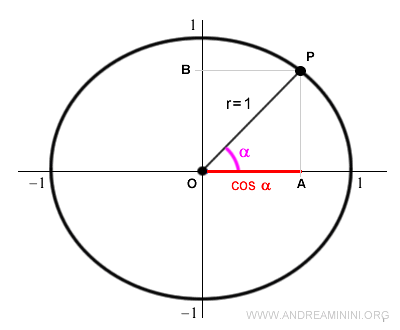
The angle α corresponds to a point P on the unit circle.
The projection of point P onto the horizontal axis gives the length of the segment OA, which is called the cosine of α.
Note: Cosine can be represented either by segment OA or segment BP, as they are equal: $$ \overline{OA} = \overline{BP} $$
In general, the cosine of an angle α is the ratio between the adjacent side of the angle and the hypotenuse in a right-angled triangle.
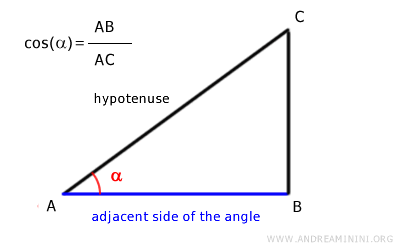
The maximum possible length of this segment equals the radius of the unit circle.
Since the unit circle has a radius of 1 (r=1), the values of the cosine function are always between -1 and 1.
Therefore, the range of the cosine function is [-1, 1].
$$ -1 \le \cos \alpha \le 1 $$
Here are some key angles and their corresponding cosine values:
| Angle (Degrees) | Angle (Radians) | Cosine |
|---|---|---|
| $$ 0° $$ | $$ 0 $$ | $$ 1 $$ |
| $$ 15° $$ | $$ \frac{\pi}{12} $$ | $$ \frac{\sqrt{6}+\sqrt{2}}{4} $$ |
| $$ 30° $$ | $$ \frac{\pi}{6} $$ | $$ \frac{\sqrt{3}}{2} $$ |
| $$ 45° $$ | $$ \frac{\pi}{4} $$ | $$ \frac{\sqrt{2}}{2} $$ |
| $$ 60° $$ | $$ \frac{\pi}{3} $$ | $$ \frac{1}{2} $$ |
| $$ 90° $$ | $$ \frac{\pi}{2} $$ | $$ 0 $$ |
| $$ 180° $$ | $$ \pi $$ | $$ -1 $$ |
| $$ 270° $$ | $$ \frac{3 \pi}{2} $$ | $$ 0 $$ |
Cosine is a periodic function with a period of 2π.
This means that 2π represents a full revolution around the unit circle, which is equivalent to a full 360° rotation.
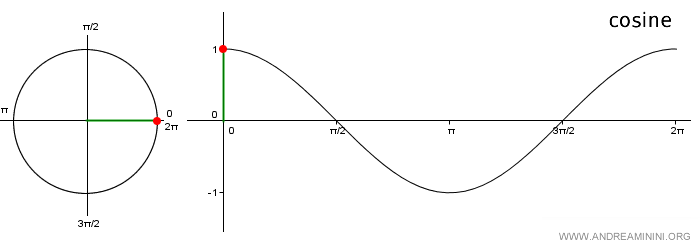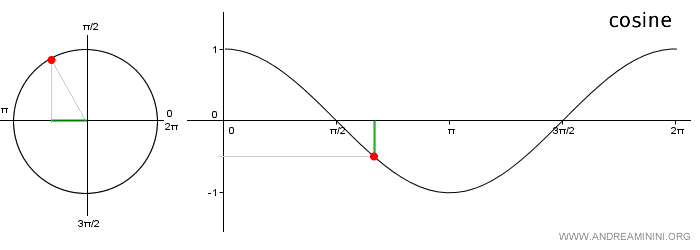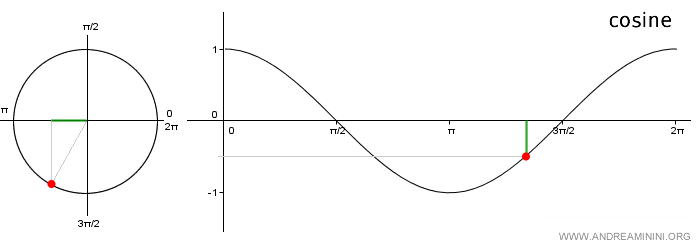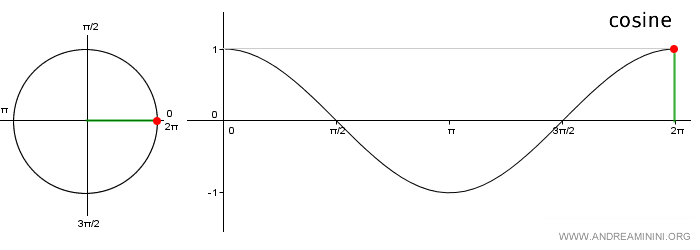
Note: The graph of the cosine function is called a cosine wave. It’s plotted by marking the angles on the x-axis and the corresponding y-values from the unit circle on the y-axis. Because it's a periodic function, you only need to consider the angles within the interval [0, 2π].
If you add one or more full rotations (2π) to a given angle α, you still end up at the same point P on the unit circle, and the cosine function will return the same value.
$$ \cos \alpha = \cos ( \alpha + n \cdot 2 \pi ) $$
For instance, both cos(0) and cos(0 + 2π) yield the value of 1.
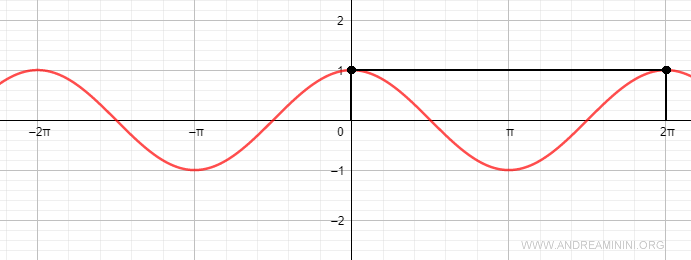
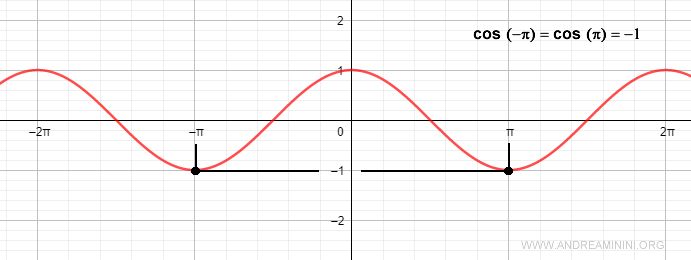
Note: From a mathematical perspective, the cosine function is an even function because $$ \cos(- \alpha) = \cos \alpha $$ This can be understood by observing the unit circle. Any oriented angle (α) and its opposite (-α) have the same projection on the horizontal x-axis.
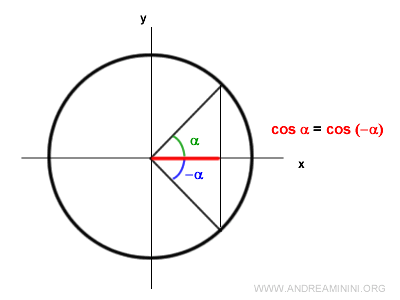
Thus, the cosine function is symmetric with respect to the y-axis. For example, the cosine of π is -1, and the cosine of -π is also -1.
The Origin of the Word "Cosine"
The Latin term "cosinus" was coined by the English mathematician and astronomer Edmund Gunter in the 17th century.
The term cosine was introduced much later than the term sine.
Although the concept of cosine was known to both the Arabs and the Greeks, they never gave it a specific name.
And so on.
