Arcsine Function
What Is the Arcsine?
The arcsine is the inverse trigonometric function of the sine within the interval [-π/2, +π/2]. It is commonly represented as arcsin or arcsin.
Occasionally, the arcsine is also denoted by sin-1, where the -1 indicates an inverse function, not an exponent. To avoid confusion, using arcsin is generally preferred.
How Does the Arcsine Work?
Given a sine value y, the arcsine calculates the corresponding angle x in radians that produces this sine value.
Example
The sine of an angle is 0.75.
$$ sin \: x = 0.75 $$
Which angle x results in this sine value?
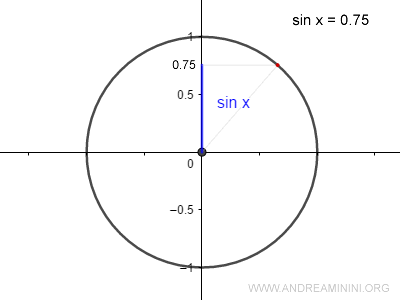
To find this angle, we calculate the arcsine of 0.75:
$$ x = arcsin (0.75) = 0.848 $$
The arcsine gives us the length x of the arc on the unit circle that corresponds to this sine value.
This arc is measured in radians and has the same magnitude as the angle x that generates the sine.
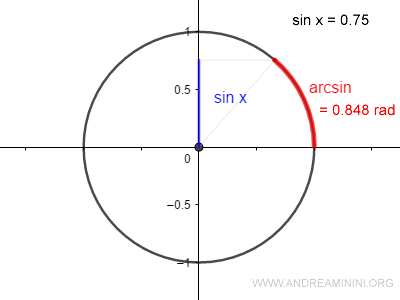
The sine function equals 0.75 when the angle x is 0.848 radians.
The Explanation
The sine function can produce values ranging from -1 to +1.
Since the sine function is periodic, the same sine value can correspond to multiple angles, or x-values.
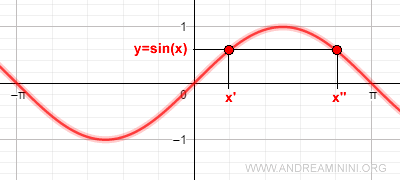
This periodic nature makes it impossible to define an inverse function for the sine over its entire domain because it would violate the principle that a function must assign a unique x to each y = f(x).
$$ f: x -> y $$
How Do We Construct the Inverse of the Sine Function?
The solution is to restrict the domain of the sine function.
By considering only a specific part of the sine’s domain, we can maintain the uniqueness of x.
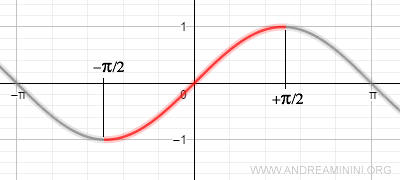
Limiting the domain to the interval [-π/2, +π/2] ensures a one-to-one correspondence between the sine values [-1, +1] and the variable x.
In this interval, the sine function is bijective, making it invertible.
This restriction allows us to construct the inverse function of the sine.
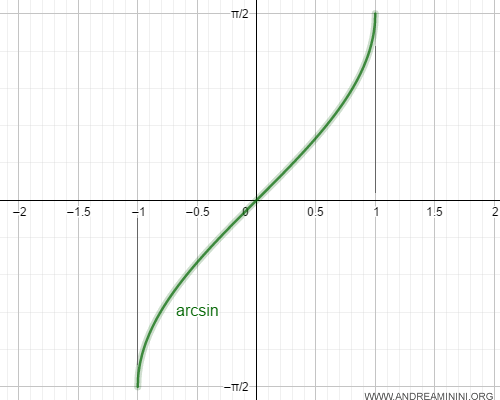
This inverse function is known as the arcsine.
$$ arcsin(x) : [-1,1] → [-π/2,π/2] $$
The notation used for arcsine is arcsin.
Starting from the sine value, the arcsine function calculates the angle x within the interval [-π/2, π/2] that corresponds to this sine.
Note: The interval [-π/2, π/2] is not the only range where the sine function can be made invertible. For example, it can also be inverted in the interval [π/2, 3π/2], as well as in infinitely many other intervals where the sine is bijective.
How to Construct the Graph of the Arcsine Function
The graph of the arcsine can be derived from the sine graph over the restricted domain [-π/2, π/2] by following two steps:
- Rotate the sine graph 90° counterclockwise.
- Reflect the graph horizontally.
The resulting graph is that of the arcsine function.
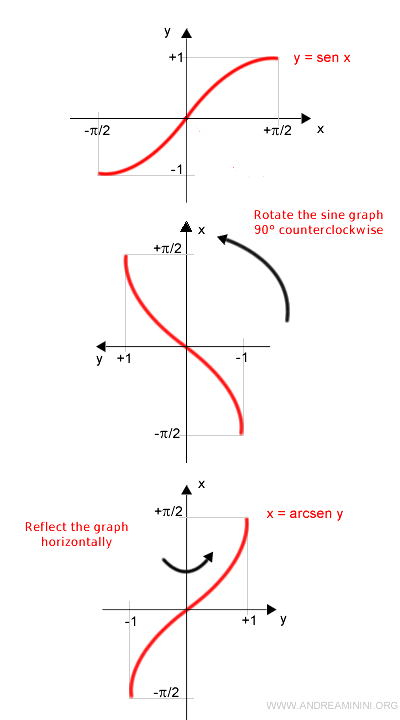
Similarly, the arcsine graph can be constructed using other restricted domains.
For example, using the interval [π/2, 3π/2] or other ranges where the sine function is invertible.
And so on.
