First Theorem of Right Triangles
- In a right triangle, the length of a leg (b) is equal to
- the hypotenuse (a) multiplied by the sine of the angle opposite (α) the leg $$ b = a \cdot \sin \alpha $$
- the hypotenuse (a) multiplied by the cosine of the adjacent acute angle (β) to the leg $$ b = a \cdot \cos \beta $$
Similarly, the other leg (c) of the right triangle is equal to the hypotenuse (a) times the sine of the opposite angle (β)
$$ c = a \cdot \sin \beta $$
and the hypotenuse (a) times the cosine of the adjacent angle (α)
$$ c = a \cdot \cos \alpha $$
A Practical Example
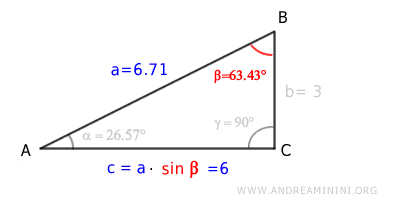
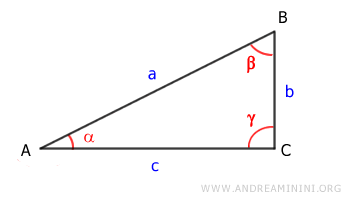
Consider a right triangle
The length of the hypotenuse is
$$ a = \overline{AB} = 6.71 $$
The lengths of the two legs are
$$ b = \overline{BC} = 3 $$
$$ c = \overline{AC} = 6 $$
The angles of the right triangle are
$$ \alpha = 26.57° $$
$$ \beta = 63.43° $$
$$ \gamma = 90° $$
When you multiply the hypotenuse (a) by the sine of angle alpha (α), you get the length of the opposite leg (b)
$$ 6.71 \cdot \sin (26.57°) = 3 $$
When you multiply the hypotenuse (a) by the cosine of alpha (α), you get the length of the adjacent leg (c)
$$ 6.71 \cdot \cos (26.57°) = 6 $$
When you multiply the hypotenuse (a) by the sine of angle beta (β), you get the length of the opposite leg (c)
$$ 6.71 \cdot \sin (63.43°) = 6 $$
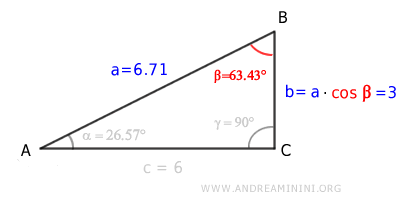
When you multiply the hypotenuse (a) by the cosine of beta (β), you get the length of the adjacent leg (b)
$$ 6.71 \cdot \cos (63.43°) = 3 $$
The Proof
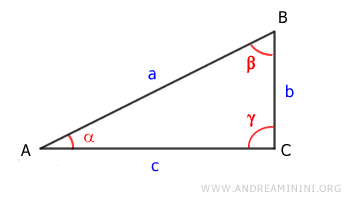
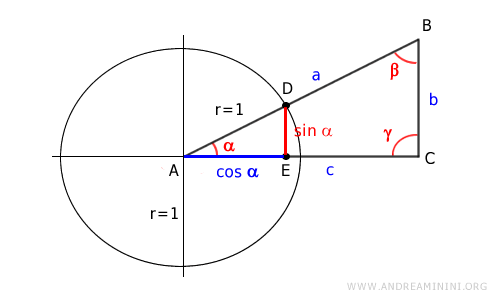
Draw a right triangle ABC where the right angle is γ.
Draw the unit circle centered at A.
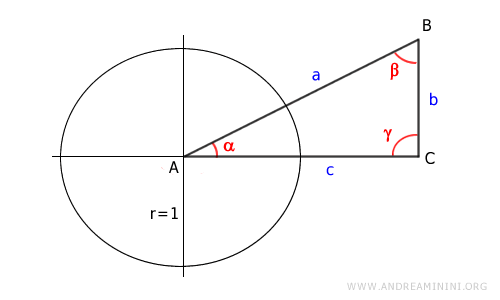
Let D be the point where the hypotenuse of the right triangle intersects the unit circle.
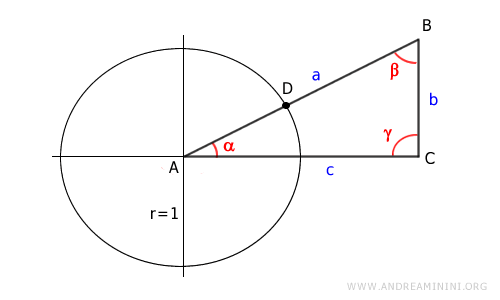
Project point D onto the x-axis (leg c) and locate point E.
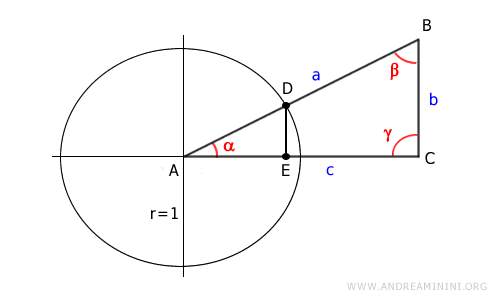
This forms another right triangle ADE inscribed in the unit circle.
Triangles ABC and ADE are similar because they are both right triangles and share the acute angle α.
Therefore, I can write the following proportion:
$$ \overline{BC} : \overline{AB} = \overline{DE} : \overline{AD} $$
$$ \overline{AC} : \overline{AB} = \overline{AE} : \overline{AD} $$
The side AD is the unit radius of the unit circle, so r = 1.
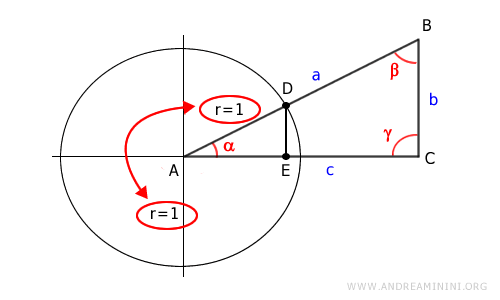
Therefore, I can replace AD with 1.
$$ \overline{BC} : \overline{AB} = \overline{DE} : 1 $$
$$ \overline{AC} : \overline{AB} = \overline{AE} : 1 $$
The side DE is the sine of angle alpha (α).
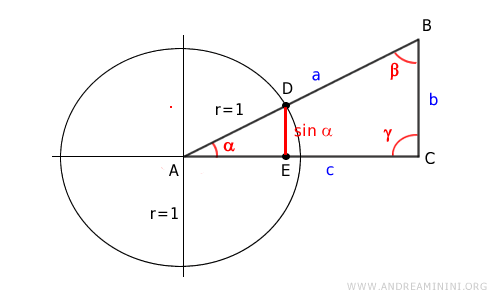
Therefore, I can replace side DE with sin α.
$$ \overline{BC} : \overline{AB} = \sin \alpha : 1 $$
$$ \overline{AC} : \overline{AB} = \overline{AE} : 1 $$
The side AE is the cosine of angle alpha (α).
Therefore, I can replace side AE with cos α.
$$ \overline{BC} : \overline{AB} = \sin \alpha : 1 $$
$$ \overline{AC} : \overline{AB} = \cos \alpha : 1 $$
Rewriting the proportions as fractions:
$$ \frac{\overline{BC}}{\overline{AB}} = \frac{\sin \alpha}{1} $$
$$ \frac{\overline{AC}}{\overline{AB}} = \frac{\cos \alpha}{1} $$
Simplify to highlight side BC and side AC:
$$ \overline{BC} = \overline{AB} \cdot \sin \alpha $$
$$ \overline{AC} = \overline{AB} \cdot \cos \alpha $$
Knowing that AB = a, BC = b, and AC = c:
$$ b = a \cdot \sin \alpha $$
$$ c = a \cdot \cos \alpha $$
Therefore, side b is equal to the hypotenuse (a) times the sine of the opposite angle (α).
Side c is equal to the hypotenuse (a) times the cosine of the adjacent angle (α).
This way, I have proven the initial theorem: the leg of a right triangle is equal to the product of the hypotenuse and the sine of the angle opposite the leg, and the product of the hypotenuse and the cosine of the angle adjacent to the leg.
Note: Consequently, following the proven theorem, side c is also equal to the product of the hypotenuse (a) and the sine of the opposite angle (β) to the leg $$ c = a \cdot \sin \beta $$ and side b is equal to the product of the hypotenuse (a) and the cosine of the adjacent angle (β) to the leg $$ b = a \cdot \cos \beta $$
All the formulas are now proven.
And so on.
