Arccotangent

The arccotangent is the inverse trigonometric function of the cotangent. It is represented as: $$ y = arccotg \ x $$ Common notations include arccotg, arccot, cotan^-1, and cotg^-1.

In geometric terms, the arccotangent measures the arc length in radians on the unit circle, which corresponds to the angle that results in the given cotangent value.

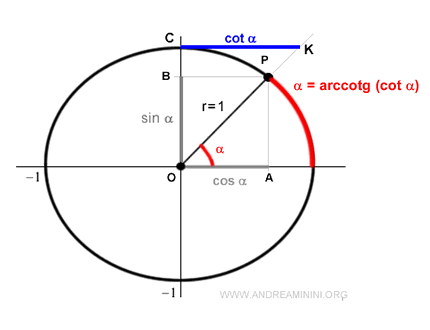
For instance, the cotangent of an angle of π/2 (90°) is zero:

$$ cotg \ \frac{\pi}{2} = 0 $$

Thus, the arccotangent of zero is π/2:

$$ arccotg \ 0 = \frac{\pi}{2} $$

Note: Since it is an inverse function, the arccotangent of a cotangent equals the angle of that cotangent. $$ arccotg ( cotg \ \alpha ) = \alpha $$

Arccotangent Function Graph

The graph of the arccotangent function is bounded between the upper limit of π and the lower limit of 0. It is a strictly decreasing function.

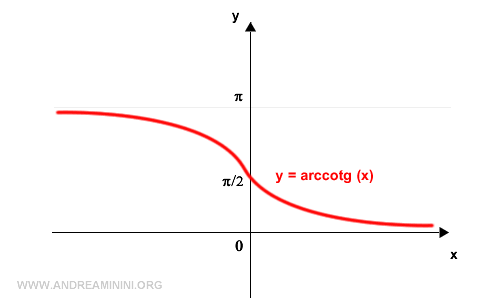
How to Construct the Arccotangent Graph

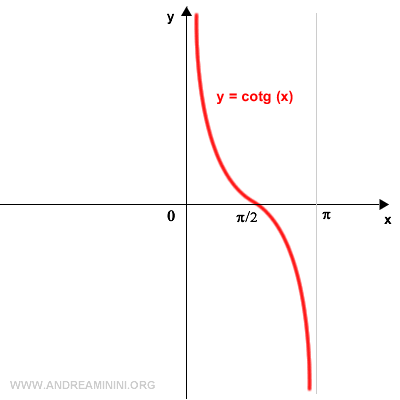
The cotangent function is periodic, which means it repeats its values at regular intervals.

Because of this periodic nature, the cotangent function is not invertible over its entire domain as it is not one-to-one (bijective).

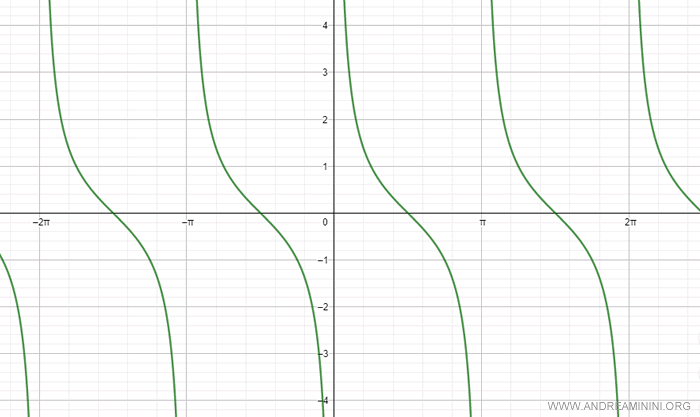
However, if we restrict the domain to the interval (0, π), the cotangent function becomes bijective (one-to-one).

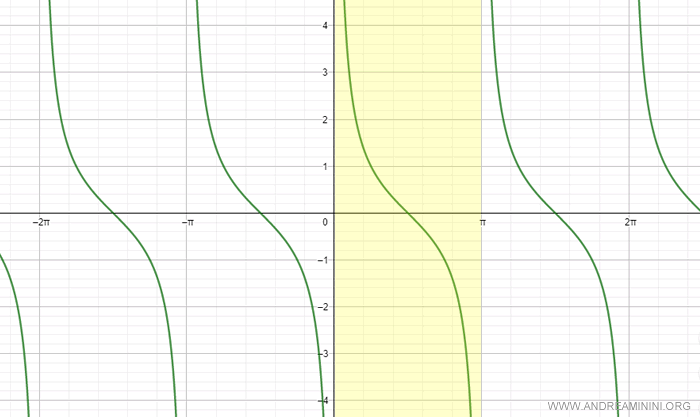
Note: The cotangent function can be bijective in other intervals as well, such as (-π, 0). Different intervals could be chosen to define the inverse function.

Since the cotangent is bijective in the interval (0, π), it is also invertible within this range.

The inverse function of the cotangent in the interval (0, π) is the arccotangent.

To obtain the arccotangent graph, rotate the cotangent graph 90° counterclockwise.

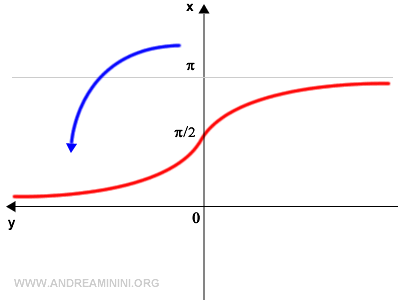
Next, reflect the graph horizontally along the vertical (x) axis.

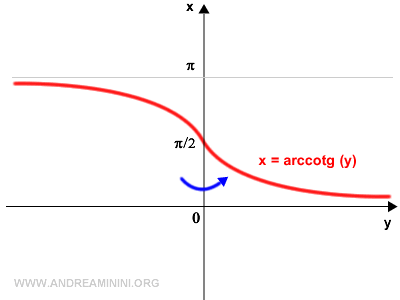
This process gives us the graph of the arccotangent.

And there you have it.