Trigonometric Functions
Trigonometric functions link the measure of an angle to the lengths of segments projected onto the axes.
For any angle α, there is exactly one point P on the circumference, defined by its intersection with the radius.
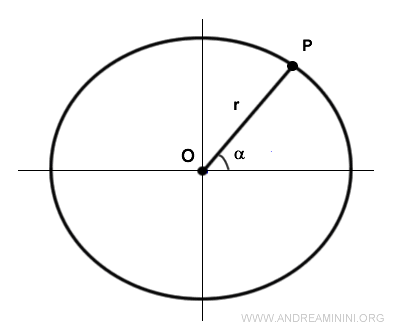
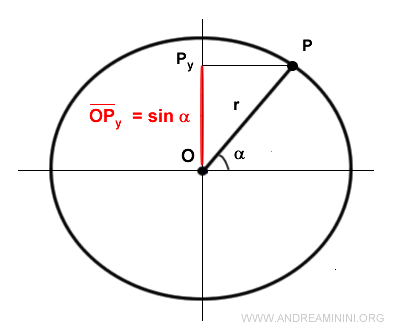
The projection of point P onto the y-axis creates a segment OPy, known as the sine.
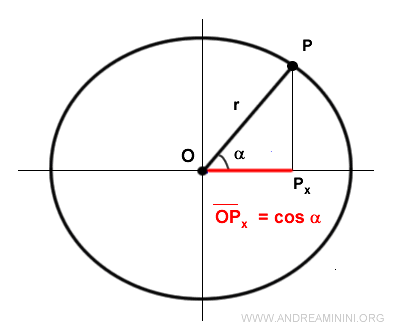
Similarly, projecting point P onto the x-axis forms a segment OPx, called the cosine.
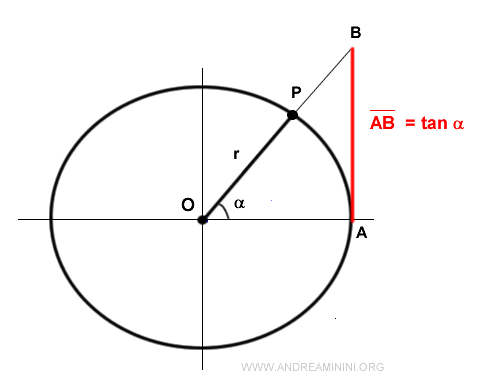
Other common trigonometric functions include the tangent and cotangent.
Key Angles
Below are some important angles for sine and cosine functions:
| Angle (Degrees) | Angle (Radians) | Sine | Cosine | Tangent | Cotangent |
|---|---|---|---|---|---|
| $$ 0° $$ | $$ 0 $$ | $$ 0 $$ | $$ 1 $$ | $$ 0 $$ | $$ \nexists $$ |
| $$ 30° $$ | $$ \frac{\pi}{6} $$ | $$ \frac{1}{2} $$ | $$ \frac{\sqrt{3}}{2} $$ | $$ \frac{\sqrt{3}}{3} $$ | $$ \sqrt{3} $$ |
| $$ 45° $$ | $$ \frac{\pi}{4} $$ | $$ \frac{\sqrt{2}}{2} $$ | $$ \frac{\sqrt{2}}{2} $$ | $$ 1 $$ | $$ 1 $$ |
| $$ 60° $$ | $$ \frac{\pi}{3} $$ | $$ \frac{\sqrt{3}}{2} $$ | $$ \frac{1}{2} $$ | $$ \sqrt{3} $$ | $$ \frac{\sqrt{3}}{3} $$ |
| $$ 90° $$ | $$ \frac{\pi}{2} $$ | $$ 1 $$ | $$ 0 $$ | $$ \nexists $$ | $$ 0 $$ |
| $$ 180° $$ | $$ \pi $$ | $$ 0 $$ | $$ -1 $$ | $$ 0 $$ | $$ \nexists $$ |
| $$ 270° $$ | $$ \frac{3 \pi}{2} $$ | $$ -1 $$ | $$ 0 $$ | $$ \nexists $$ | $$ 0 $$ |
The cosine is a periodic function with a period of 2π.
The Period of Trigonometric Functions
Trigonometric functions repeat at regular intervals, known as their periods.
Some functions share the same period length.
| Function | Period |
|---|---|
| $$ \sin x $$ | $$ 2 \pi $$ |
| $$ \cos x $$ | $$ 2 \pi $$ |
| $$ \sin (\omega x + \phi) $$ | $$ \frac{2 \pi}{\omega} $$ |
| $$ \cos (\omega x + \phi) $$ | $$ \frac{2 \pi}{\omega} $$ |
| $$ \tan x $$ | $$ \pi $$ |
| $$ \cot x $$ | $$ \pi $$ |
| $$ \tan (\omega x + \phi) $$ | $$ \frac{\pi}{\omega} $$ |
| $$ \cot (\omega x + \phi) $$ | $$ \frac{\pi}{\omega} $$ |
And so on.
