Associated Angles in Trigonometry
Associated angles are angles expressed in radians that have the same trigonometric function values in absolute terms. They are also known as associated arcs.
A practical example
The sine of angle α is equal to the absolute value of the sine of -α.
$$ \sin(\alpha) = |\sin(-\alpha)| $$
Therefore, angles α and -α are associated angles for the sine function because they yield the same absolute value.
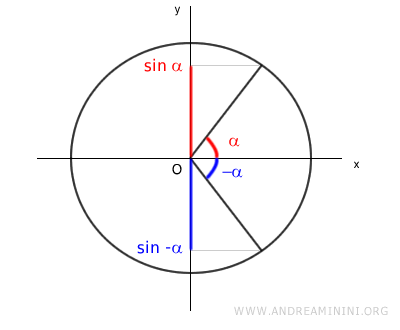
Knowing that the sine function is odd, f(-x) = -f(x), we can calculate the sine of -α using the associated angle α.
$$ \sin(-\alpha) = -\sin(\alpha) $$
Note: Angles α and -α are also associated angles for the cosine function. $$ \cos(\alpha) = |\cos(-\alpha)| $$ Both functions return the same absolute value for cosine.
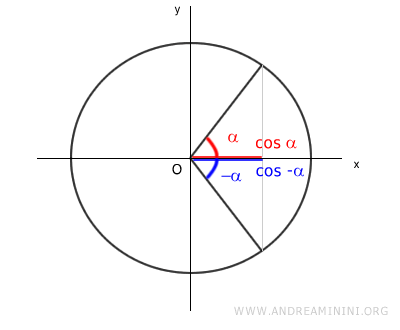
Since cosine is an even function, f(-x) = f(x), the cosine of -α can also be found using the associated angle: $$ \cos(\alpha) = \cos(-\alpha) $$
What are they used for?
In trigonometry, associated angles allow us to reduce trigonometric functions with arguments in other quadrants (π/2; 2π) to the first quadrant (0; π/2).
Reducing to the first quadrant simplifies calculations.
Example: To calculate the cosine of -20°, $$ \cos(-20°) $$, which is in the IV quadrant. Knowing that cosine has the same value for opposite angles, we can reduce the formula to the first quadrant: $$ \cos(-20°) = \cos(20°) $$
Formulas for Associated Angles
Here are the main formulas for associated angles in trigonometry:
| Associated Angles | Formulas | Proof |
|---|---|---|
| $$ \alpha \ \ , \ \ -\alpha $$ | $$ \sin(-\alpha) = -\sin(\alpha) $$ $$ \cos(-\alpha) = \cos(\alpha) $$ $$ \tan(-\alpha) = -\tan(\alpha) $$ $$ \cot(-\alpha) = -\cot(\alpha) $$ | see explanation |
| $$ \alpha \ \ , \ \ \pi + \alpha $$ | $$ \sin(\pi+\alpha) = -\sin(\alpha) $$ $$ \cos(\pi+\alpha) = -\cos(\alpha) $$ $$ \tan(\pi+\alpha) = \tan(\alpha) $$ $$ \cot(\pi+\alpha) = \cot(\alpha) $$ | see explanation |
| $$ \alpha \ \ , \ \ \pi - \alpha $$ | $$ \sin(\pi-\alpha) = \sin(\alpha) $$ $$ \cos(\pi-\alpha) = -\cos(\alpha) $$ $$ -\tan(\pi-\alpha) = \tan(\alpha) $$ $$ -\cot(\pi-\alpha) = \cot(\alpha) $$ | see explanation |
| $$ \alpha \ \ , \ \ 2\pi - \alpha $$ | $$ \sin(2\pi-\alpha) = -\sin(\alpha) $$ $$ \cos(2\pi-\alpha) = \cos(\alpha) $$ $$ -\tan(2\pi-\alpha) = \tan(\alpha) $$ $$ -\cot(2\pi-\alpha) = \cot(\alpha) $$ | see explanation |
| $$ \alpha \ \ , \ \ \frac{\pi}{2} + \alpha $$ | $$ \sin(\frac{\pi}{2} + \alpha) = \cos(\alpha) $$ $$ \cos(\frac{\pi}{2} + \alpha) = -\sin(\alpha) $$ $$ \tan(\frac{\pi}{2} + \alpha) = -\cot(\alpha) $$ $$ \cot(\frac{\pi}{2} + \alpha) = -\tan(\alpha) $$ | see explanation |
| $$ \alpha \ \ , \ \ \frac{\pi}{2} - \alpha $$ | $$ \sin(\frac{\pi}{2} - \alpha) = \cos(\alpha) $$ $$ \cos(\frac{\pi}{2} - \alpha) = \sin(\alpha) $$ $$ \tan(\frac{\pi}{2} - \alpha) = \cot(\alpha) $$ $$ \cot(\frac{\pi}{2} - \alpha) = \tan(\alpha) $$ | see explanation |
| $$ \alpha \ \ , \ \ \frac{3\pi}{2} + \alpha $$ | $$ \sin(\frac{3\pi}{2} + \alpha) = -\cos(\alpha) $$ $$ \cos(\frac{3\pi}{2} + \alpha) = \sin(\alpha) $$ $$ \tan(\frac{3\pi}{2} + \alpha) = -\cot(\alpha) $$ $$ \cot(\frac{3\pi}{2} + \alpha) = -\tan(\alpha) $$ | see explanation |
| $$ \alpha \ \ , \ \ \frac{3\pi}{2} - \alpha $$ | $$ \sin(\frac{3\pi}{2} - \alpha) = -\cos(\alpha) $$ $$ \cos(\frac{3\pi}{2} - \alpha) = -\sin(\alpha) $$ $$ \tan(\frac{3\pi}{2} - \alpha) = \cot(\alpha) $$ $$ \cot(\frac{3\pi}{2} - \alpha) = \tan(\alpha) $$ | see explanation |
And so on.
