Associated Angles α and π+α

In trigonometry, the angles alpha (α) and π+α allow us to apply the following transformation formulas: $$ \sin(\pi+\alpha) = -\sin(\alpha) $$ $$ \cos(\pi+\alpha) = -\cos(\alpha) $$ $$ \tan(\pi+\alpha) = \tan(\alpha) $$ $$ \cot(\pi+\alpha) = \cot(\alpha) $$

As associated angles, α and π+α have the same absolute values for the trigonometric functions (sine, cosine, tangent, and cotangent).

Proof and Explanation

Let's consider an angle α and its associated angle π+α on a unit circle.

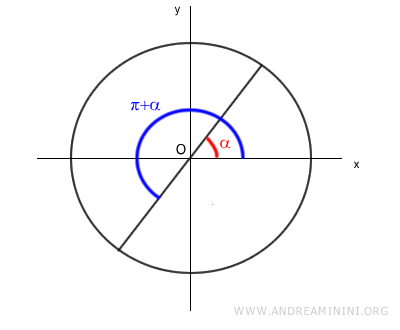
The difference between α and π+α is a straight angle of 180° (π).

$$ (\pi + \alpha) - \alpha = \pi $$

Now, let's construct two right triangles, OAB and OCD.

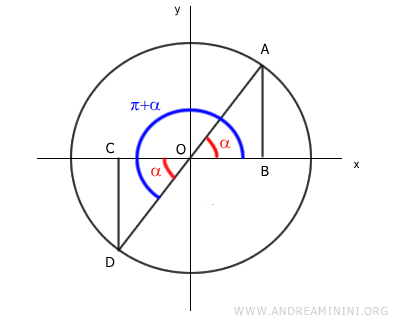
The right triangles OAB and OCD are congruent (identical) since they share the same hypotenuse (OA = OC) and have the same acute angle (α) as well as a right angle (90°).

Because of this, the two triangles have equal angles and side lengths.

Therefore, α and π+α have the same absolute value for the sine function, as the heights of the triangles are equal, AB = CD.

$$ \sin \alpha = | \sin (\pi + \alpha) | $$

Visually speaking:

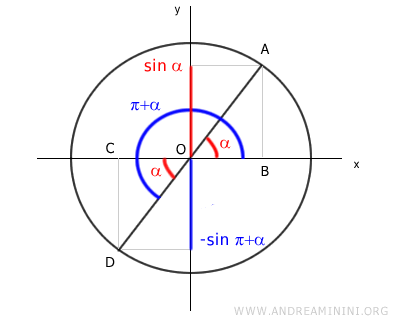
However, AB is on the positive y-axis, while CD is on the negative y-axis.

Thus, the sine of the associated angles α and π+α have opposite signs.

$$ \sin \alpha = - \sin (\pi + \alpha) $$

Note: By multiplying both sides of the equation by -1, we can also express the relationship in reverse: $$ (-1) \cdot \sin \alpha = (-1) \cdot (- \sin (\pi + \alpha)) $$ $$ - \sin \alpha = \sin (\pi + \alpha) $$

Similarly, α and π+α have the same absolute value for the cosine function, as OB = OD.

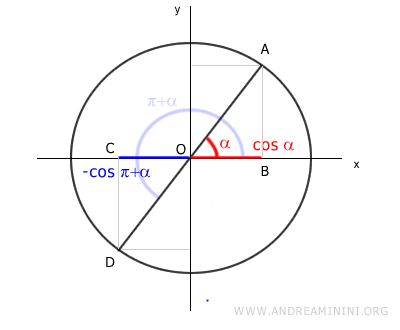
Here again, the cosine values are opposite, since OC lies on the negative x-axis and OB on the positive x-axis.

$$ \cos \alpha = - \cos (\pi + \alpha) $$

Note: By multiplying both sides of the equation by -1, we can also express this in reverse: $$ (-1) \cdot \cos \alpha = (-1) \cdot ( - \cos (\pi + \alpha) ) $$ $$ - \cos \alpha = \cos (\pi + \alpha) $$

Thus, the cosine of the associated angles α and π+α have opposite signs.

At this point, we can derive the transformation formulas for tangent and cotangent.

The tangent is defined as the ratio between sine and cosine.

$$ \tan (\pi + \alpha) = \frac{ \sin (\pi + \alpha) }{ \cos (\pi + \alpha) } $$

Knowing that sin(π+α) = -sin(α) and cos(π+α) = -cos(α), we have:

$$ \tan (\pi + \alpha) = \frac{ - \sin \alpha }{ - \cos \alpha } = \tan \alpha $$

So, the tangent of π+α is equal to the tangent of α.

The cotangent is defined as the ratio between cosine and sine.

$$ \cot (\pi + \alpha) = \frac{ \cos (\pi + \alpha) }{ \sin (\pi + \alpha) } $$

Since sin(π+α) = -sin(α) and cos(π+α) = -cos(α), we get:

$$ \cot (\pi + \alpha) = \frac{ - \cos \alpha }{ - \sin \alpha } = \cot \alpha $$

Therefore, the cotangent of π+α is equal to the cotangent of α.

In conclusion, the associated angles α and π+α have the same values for tangent and cotangent.

A Practical Example

Let's calculate the sine of 210°:

$$ \sin 210° $$

We can rewrite 210° as the sum of 180° + 30°:

$$ \sin 210° = \sin (180° + 30°) $$

In radians, this becomes:

$$ \sin 210° = \sin \left( \pi + \frac{\pi}{6} \right) $$

The angles π+α and α are associated, where α = π/6 (or 30°).

$$ \sin (\pi + \alpha) = -\sin(\alpha) $$

Thus, the sine of 210° is the negative of the sine of 30°:

$$ \sin 210° = \sin \left( \pi + \frac{\pi}{6} \right) = -\sin \left( \frac{\pi}{6} \right) $$

Since the sine of 30° is 1/2, the sine of 210° is -1/2.

$$ \sin 210° = - \frac{1}{2} $$

And so on.