Cotangent

In the unit circle, the cotangent of an angle alpha is the reciprocal of the tangent, defined as the ratio of the cosine to the sine of angle alpha. $$ \cot \ \alpha = \frac{1}{\tan \alpha} = \frac{\cos \alpha}{\sin \alpha} $$ It is represented by the symbols cot, ctg, or cotg.

From a geometric perspective, the cotangent corresponds to the segment CK.

This is obtained by extending the radius OP until it intersects at point K with a line parallel to the x-axis, which is tangent to the unit circle at CK.

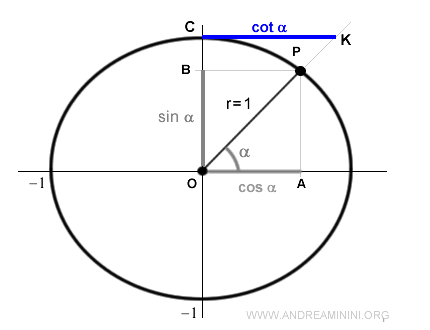
By definition, the cotangent is the ratio between the x-coordinate OA and the y-coordinate OB of point P.

Other formulas are derived from this definition.

$$ cotg \ \alpha = \frac{\overline{OA}}{\overline{OB}} = \frac{\cos \alpha}{\sin \alpha} = \frac{1}{\tan \alpha} $$

Here, segment OA represents the cosine, and segment OB represents the sine of the angle α that defines point P.

Note. The cotangent is undefined at angles where the y-coordinate (sine) is zero. At these points, division by zero occurs, resulting in an undefined ratio. Therefore, the cotangent is not defined at angles where the sine is zero.

The term "cotangent" was first introduced by the English mathematician Edmund Gunter in the 17th century.

Properties of the Cotangent Function

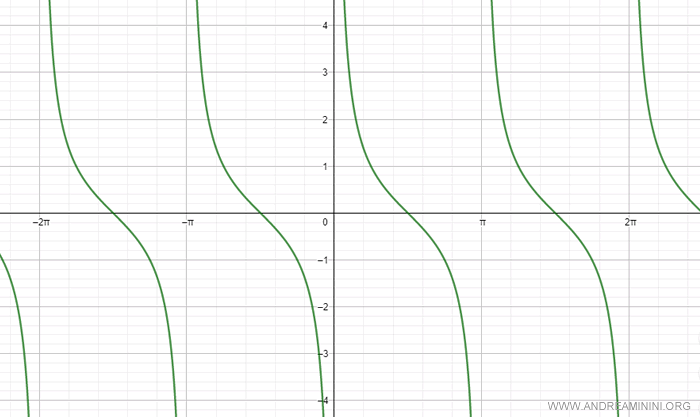
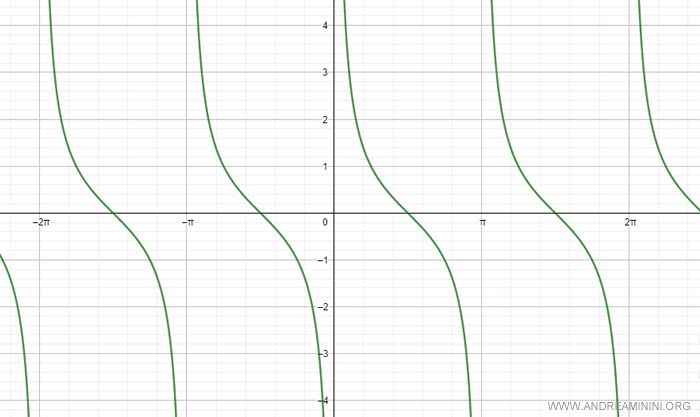
The cotangent is a periodic function that repeats every π (or 180°).

$$ cotg \ \alpha = \cot( \alpha + n \cdot \pi ) $$

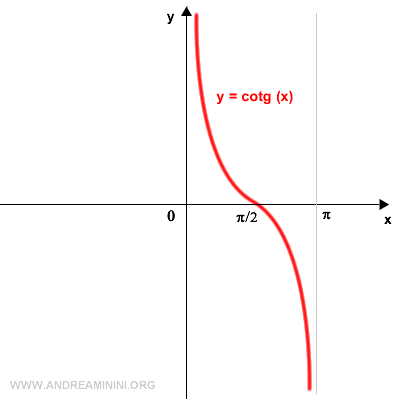
Below is the graph of the cotangent from -2π to 2π.

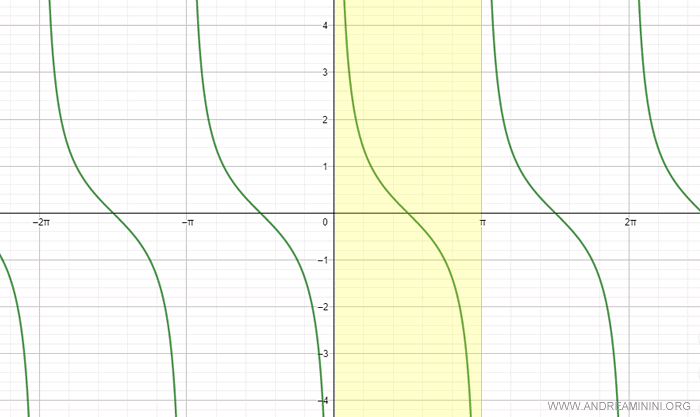
Note. Since the cotangent is a periodic function with a period of π, it can be studied within the interval (0, π). In this interval, the cotangent is a continuous, monotonic, and decreasing function.

The cotangent is undefined at angles 0 and at multiples of k·π, where k is an integer, due to the sine in the denominator being zero (sin 0=0).

$$ \alpha = k \cdot \pi $$

The graph of the cotangent shows vertical asymptotes at the angles α=k·π, where the cotangent is not defined.

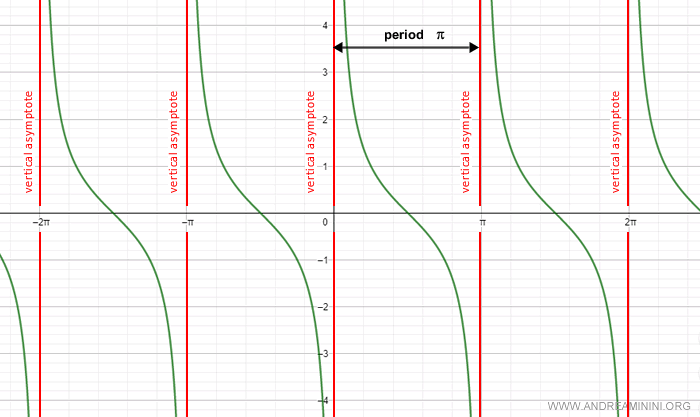
The domain of the cotangent function includes all real numbers, except for integer multiples of π.

$$ cotg \ \alpha : \ R \ - \ k \cdot \pi \ \ \rightarrow R \ \ \ \ with \ k \in Z $$

The codomain is the set of all real numbers.

Hence, the value of the cotangent ranges from -∞ to +∞.

Key Angles of the Cotangent

The table below lists the primary angles of the cotangent.

Degrees	Radians	Cotangent
0°	0	undefined
15°	π/12	2 + √3
30°	π/6	√3
45°	π/4	1
60°	π/3	(√3)/3
75°	5π/12	2 - √3
90°	π/2	0
180°	π	undefined
270°	3π/2	0
360°	2π	undefined

The Proof

Consider an angle α that defines a point P on the unit circle.

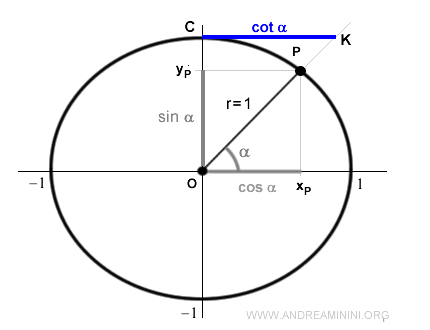
The cotangent is the function that associates the angle α with the ratio of the x-coordinate x_P to the y-coordinate y_P of point P.

$$ cotg \ \alpha = \frac{x_P}{y_P} $$

In the unit circle, the x-coordinate x_P is the cosine, while the y-coordinate y_P is the sine.

$$ cotg \ \alpha = \frac{x_P}{y_P} = \frac{\cos \alpha}{\sin \alpha} $$

Since the tangent is defined as the ratio of sine to cosine, tan = sin/cos, the reciprocal of the tangent is 1/tan = cos/sin.

Thus, the cotangent can also be expressed as the reciprocal of the tangent.

$$ cotg \ \alpha = \frac{x_P}{y_P} = \frac{\cos \alpha}{\sin \alpha} = \frac{1}{\tan \alpha} $$

Note. The equality between the cotangent and the reciprocal of the tangent holds only when the angle alpha is not a multiple of π or π/2: $$ cotg \ \alpha = \frac{1}{\tan \alpha} \ \ \ , with \ \alpha \ne k \cdot \frac{\pi}{2} $$ because at multiples of π, the cotangent is not defined, while at multiples of π/2, the tangent is not defined. Therefore, this equality applies to a subset of the cotangent's domain.

Geometric Proof

Let's consider any oriented angle that is neither π nor π/2.

In the unit circle, the triangles are similar since they share the same angles.

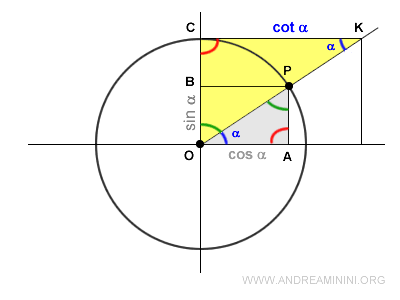
Because the triangles are similar, a proportion exists between the corresponding sides:

$$ \overline{CK} \ : \ \overline{OA} = \overline{OC} \ : \ \overline{AP} $$

or equivalently:

$$ \frac{ \overline{CK} }{ \overline{OA} } = \frac{ \overline{OC} }{ \overline{AP} } $$

Knowing that the segment CK is the cotangent of angle α:

$$ \frac{ cotg \ \ alpha }{ \overline{OA} } = \frac{ \overline{OC} }{ \overline{AP} } $$

The segment OC equals the radius of the unit circle, r = 1.

$$ \frac{ cotg \ \alpha }{ \cos \alpha } = \frac{ 1 }{ \sin \alpha } $$

Highlighting the cotangent, we obtain the formula to be proven:

$$ cotg \ \alpha = \frac{ \cos \alpha }{ \sin \alpha } $$

The Inverse Function of the Cotangent

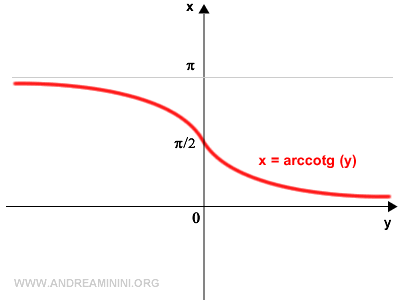
The inverse function of the cotangent is the arccotangent.

The cotangent is not invertible over its entire domain because it is a periodic function.

However, by restricting its domain to the interval (0, π), the cotangent becomes bijective.

Note. There are infinite intervals where the cotangent function is bijective, such as (-π, 0) or (π, 2π). Generally, the interval (0, π) is used, but other intervals can be chosen if needed.

Within the interval (0, π), the cotangent is an invertible function.

To obtain the graph of the inverse function, rotate the graph 90° counterclockwise.

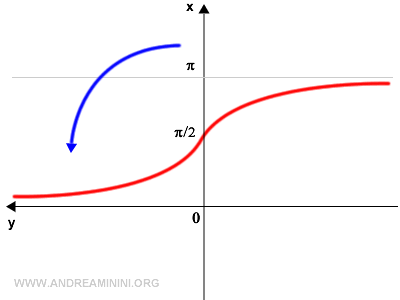
Next, reflect the graph horizontally over the vertical axis.

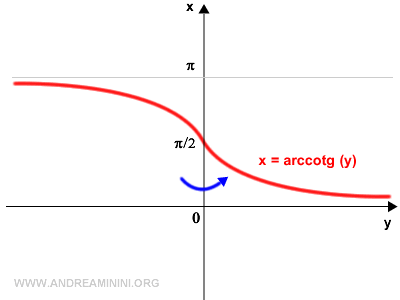
This results in the graph of the inverse function of the cotangent, known as the arccotangent.

And so on.