Second Fundamental Law of Trigonometry

The tangent of an angle is the ratio of the sine to the cosine of that angle. $$ \tan \alpha = \frac{ \sin \alpha }{ \cos \alpha } $$

Proof

Let's consider an angle alpha on the unit circle.

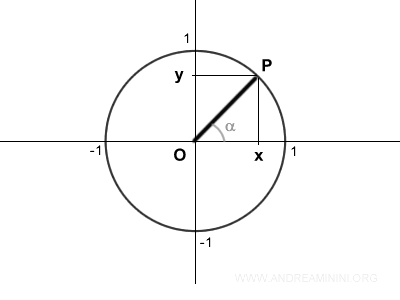
The segment OP lies on the line r.

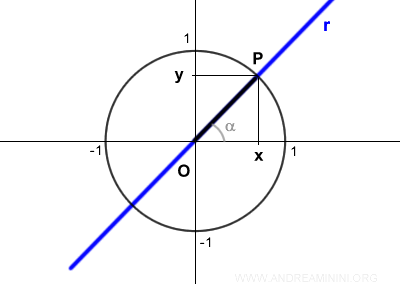
The equation of a line passing through the origin is y = mx, where m is the slope, which determines the line's inclination.

$$ y = m \cdot x $$

Now, multiplying both sides of the equation by 1/x isolates the slope:

$$ y \cdot \frac{1}{x} = m \cdot x \cdot \frac{1}{x} $$

After simplifying:

$$ \frac{y}{x} = m $$

We see that the slope (m) of the line r is the ratio y/x.

$$ m = \frac{y}{x} $$

Since the slope of the line is equivalent to the tangent of angle alpha (see this explanation):

$$ m = \frac{y}{x} = \tan \alpha $$

On the unit circle, y corresponds to sin α, and x corresponds to cos α.

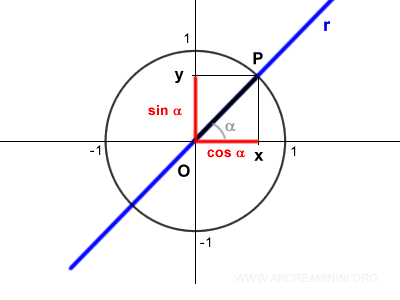
Thus, we can express this as:

$$ m = \frac{y}{x} = \frac{\sin \alpha}{ \cos \alpha } = \tan \alpha $$

In this way, we've proven the second fundamental law of trigonometry.

$$ \frac{\sin \alpha}{ \cos \alpha } = \tan \alpha $$

And that's the result.