Relationship between the tangent and the slope of a line

The slope of a line y = mx + q is equal to the tangent of the angle α between the line and the horizontal x-axis: $$ m = \tan \alpha$$

Visually:

Proof

To keep things simple, let's consider a line that passes through the origin, which means q=0.

$$ y = mx + q \ \ \ \ \ \ where \ q=0 $$

$$ y = mx $$

We can now plot the line on a Cartesian plane.

Let’s emphasize the slope m.

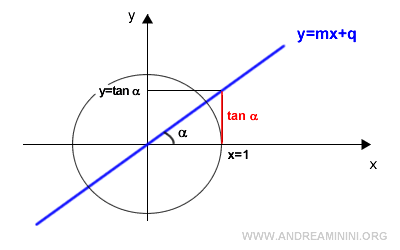
$$ m = \frac{y}{x} $$

In a unit circle, the radius is 1, so x=1.

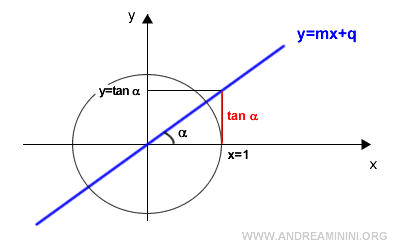
At the same time, y is the tangent of the angle alpha, meaning y = tan α.

The angle alpha is the one between the line and the x-axis.

$$ m = \frac{y}{x} $$

$$ m = \frac{\tan \alpha}{1} $$

$$ m = \tan \alpha $$

Therefore, the slope of the line is equal to the tangent of the directed angle between the line and the x-axis.

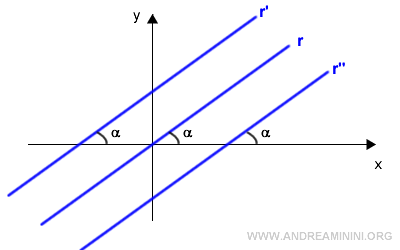
Note: This result holds even if the line doesn’t pass through the origin (q≠0). All parallel lines form the same angle with the x-axis. Since parallel lines share the same angle α, they also have the same tangent value, tan α. Thus, parallel lines have the same slope m = tan α.

And so on.