Directed Angle

What is a Directed Angle?

A directed angle is an angle between two sides associated with a direction of rotation.

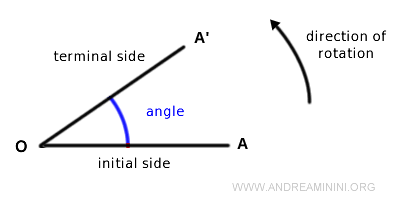
In a directed angle, the sides are considered in a specific order. The initial side is called the initial side, and the final side after rotation is called the terminal side.

Generally, by convention, the angle is positive if the rotation is counterclockwise and negative if it is clockwise.

The zero initial side is considered the positive x-axis of the Cartesian plane.

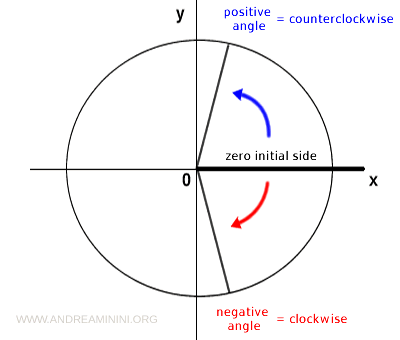
Note: To indicate an angle α less than a full turn and all the infinite directed angles obtained after completing a full turn, I use the notation in degrees $$ \alpha + k \cdot 360° \ \ \ with \ k \in Z $$ or in radians $$ \alpha + k \cdot 2 \pi \ \ \ with \ k \in Z $$ For example, to indicate the angle α = 800°, I use k = 2 and write $$ \alpha = 80° + 360 \cdot 2 $$

A Practical Example

Let's consider a directed angle as an example.

$$ a \hat{O} b $$

The initial side is side "a," while the terminal side is side "b." The vertex is point O.

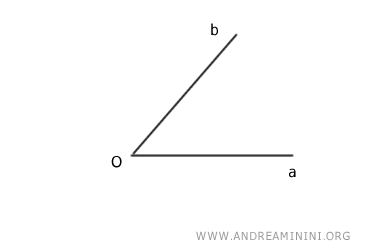
What is the measure of this directed angle?

Since it's a directed angle, I can't say anything yet because I haven't indicated the direction of the angle.

There are two possibilities:

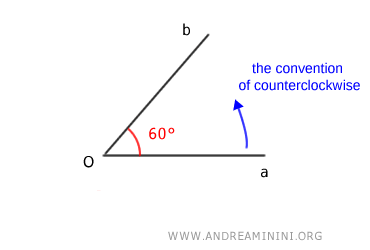
If the angle is oriented counterclockwise, the angle measures 60°

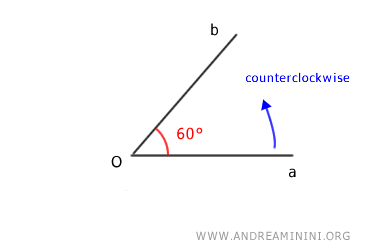
Conversely, if the angle is oriented clockwise, the angle measures 300°

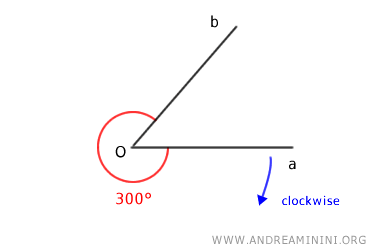
In both cases, side "a" is the initial side (or initial side) of the directed angle, but the measure is entirely different.

Therefore, the measure of a directed angle depends solely on the direction assigned to it.

Note: To avoid confusion, when a direction is not indicated in a directed angle, the counterclockwise direction is conventionally used to measure the angle. Therefore, in this example, the directed angle has a measure of 60° by convention.

Positive and Negative Angles

The positive or negative sign of a directed angle depends on the movement of segment OA and the direction of rotation adopted as the reference system.

• If I adopt the counterclockwise direction as the reference, the directed angle is positive when it rotates counterclockwise and negative when it rotates clockwise.
  

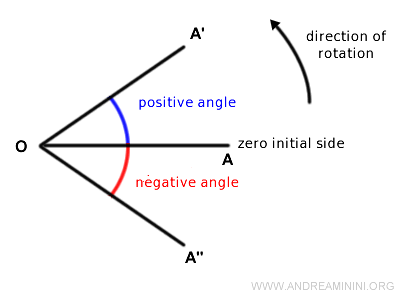
  Note: In this case, the rotation of the segment from OA to OA' is in line with the reference rotation direction. Therefore, the angle is positive. Conversely, the rotation of the segment from OA to OA" is not in line, making the angle negative.

• If I adopt the clockwise direction as the reference, the directed angle is positive when it rotates clockwise and negative when it rotates counterclockwise.
  

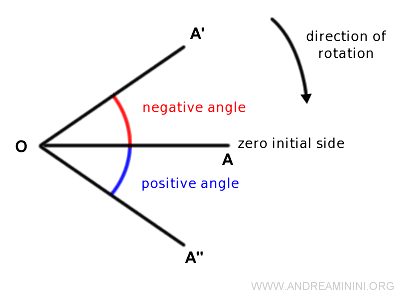
  Note: In this case, the rotation of the segment from OA to OA" is in line with the reference rotation direction. Therefore, the angle is positive. Conversely, the rotation of the segment from OA to OA' is not in line, making the angle negative.

What happens if the reference rotation direction is missing?

If a rotation direction is not specified as a reference system, in physics and mathematics, the counterclockwise direction with the initial side on the positive x-axis is conventionally adopted.

Therefore, the directed angle is positive if the segment rotates counterclockwise, and negative if it rotates clockwise.

What are Directed Angles Used For?

In many cases, the measure of an angle does not provide all the information I need.

For example, I need to turn the rudder by 30°. But in which direction? To the right or to the left?

 

To know this, I first need to establish a rotation direction as a reference system.

I adopt the counterclockwise direction.

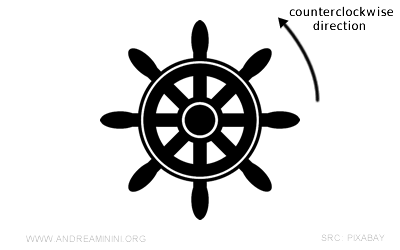
This way, I can understand the rotation direction.

Since 30° is a positive number, it means that the direction is consistent with the rotation direction.

So, I turn the rudder counterclockwise, or to the left.

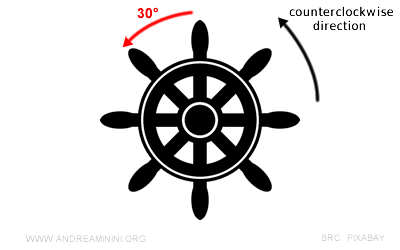
If the directed angle had been -30°, I would have had to turn the rudder to the right because it would not be consistent with the reference rotation direction.

Characteristics of Directed Angles

Directed angles have two distinguishing characteristics:

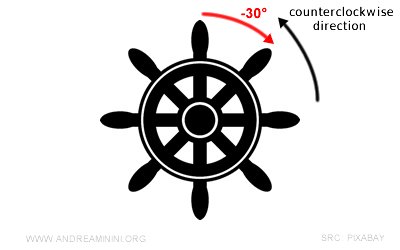
• Directed angles can have a negative measure
  An angle is negative when it is not consistent with the adopted reference rotation direction. For example, an angle of -20°.
  
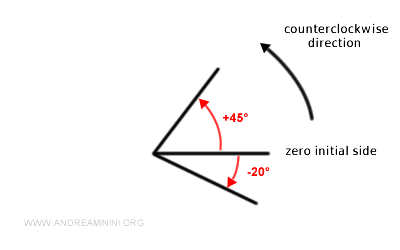
• Directed angles can also be greater than a full turn of 360° (2π radians)
  For example, a directed angle of 730° means that I must make two complete turns in the adopted reference rotation direction and add another 10°.
  
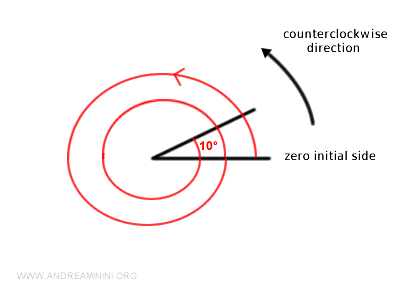
  Algebraically, $$ 730° = 360° \cdot 2 + 10° $$ $$ 730° = 720° + 10° $$

Simplified Notation for Directed Angles

A directed angle greater than 360° can be written in a simplified form as the sum of an angle less than 360° and a full turn multiplied by a scalar k. $$ \alpha° + 360° \cdot k $$ If the angle is in radians, 2π is used.$$ \alpha + 2 \pi \cdot k $$ In both cases, k is an integer.

If k is not specified, the notation considers all directed angles that differ by a multiple k of the full turn.

Where k is a positive or negative integer.

Example 1

A directed angle of 730° can be written as

$$ 730° = 360° \cdot 2 + 10° $$

Where k=2

Example 2

If I do not specify the scalar k

$$ \frac{ \pi }{ 2 } + k \cdot 2 \pi $$

the notation indicates all angles of 90° (or π/2) that are multiples of a full turn (2π)

$$ \frac{ \pi }{ 2 } + k \cdot 2 \pi = \{ \frac{ \pi }{ 2 } \ , \ \frac{ \pi }{ 2 } \pm 2 \pi \ , \ \frac{ \ pi }{ 2 } \pm 4 \ pi \ , \ ... \} $$

Here is a graphical representation of π/2 (blue) and π/2 + 2π (red).

In the first case, k = 0, while in the second case, k = 1.

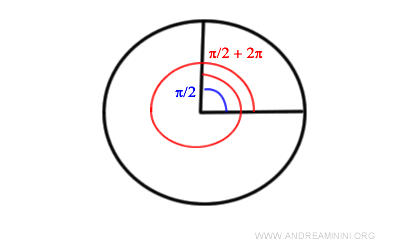
And so on.