Corresponding Angles

Corresponding angles are pairs of angles that do not share a common vertex and are situated in the same relative position with respect to two lines intersected by a transversal.

In other words, corresponding angles are angles that occupy the same "position."

In each pair of corresponding angles, one angle is exterior, while the other is interior.

A Practical Example

Here is a practical example.

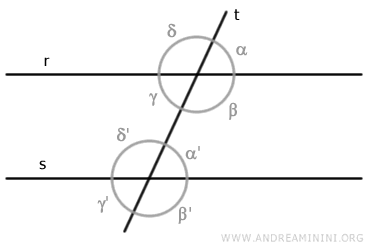
Consider two lines “r” and “s” cut by a transversal line “t”.

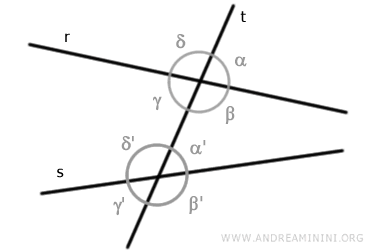
The intersections between line “t” and the other two lines form eight angles: α, β, γ, δ, α', β', γ', δ'

Corresponding angles are pairs of angles that are in the same position relative to line "t" and do not share a common vertex.

For example, angles α and α' are corresponding angles.

Angle α is on the exterior side of the lines, while angle α' is on the interior side.

Similarly, angles β and β' are corresponding angles.

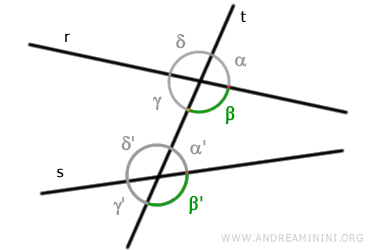
Likewise, angles γ and γ' form another pair of corresponding angles.

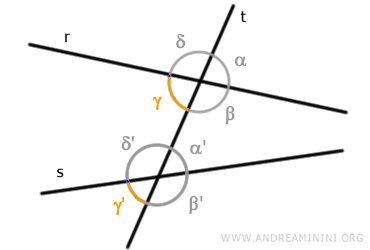
Finally, angles δ and δ' are the last pair of corresponding angles.

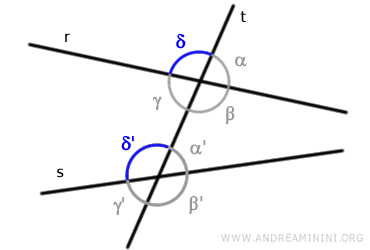
In all these cases, one angle of the pair is inside lines "r" and "s," while the other is outside.

The Case of Parallel Lines

When lines "r" and "s" are parallel and intersected by a transversal "t," the corresponding angles are also congruent, meaning they have the same measure.

For instance, in this case, angles α and α' are not only corresponding angles but also congruent because they have the same measure.

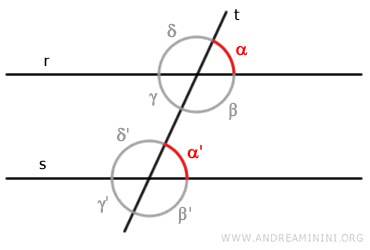
This is one of the fundamental properties of parallel lines in Euclidean geometry and is often used in geometric proofs and theorems.