Adding or Subtracting Congruent Angles

If two angles are formed by adding (or subtracting) pairs of congruent angles in corresponding positions, then the resulting angles are also congruent.

In other words, if we have two pairs of congruent angles:

$$ α ≅ β $$

$$ γ ≅ δ  $$

Then the sum of the corresponding angles will also be congruent:

$$ α + γ ≅ β + δ $$

The same holds for the difference:

$$ |α − γ| ≅ |β − δ| $$

This is because congruence is preserved when we perform operations on equal measures:

Note. Two angles are congruent when they have the same measure - that is, when they perfectly overlap if superimposed, regardless of their position on the plane.

Practical Examples

Let’s take two pairs of congruent angles: $ \alpha \cong \beta = 45° $ and $ \gamma \cong \delta = 30° $. 

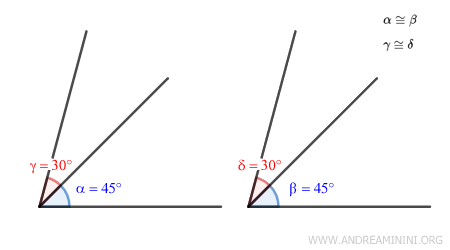
The sum of the angles α + γ and β + δ is the same: 75°.

$$ α + γ = 45° + 30° = 75° $$

$$ β + δ = 45° + 30° = 75° $$

The same goes for subtraction: both α - γ and β - δ equal 15°.

$$ α - γ = 45° - 30° = 15° $$

$$ β - δ = 45° - 30° = 15° $$

So, whether you’re adding or subtracting pairs of congruent angles, the result will still be congruent.

Note. This property is particularly useful in geometry, especially when working with angles formed through construction or translation. It also allows us to treat angle expressions algebraically, focusing on their measure rather than their position in the plane.

Proof

Let’s start with two pairs of congruent angles:

$$ \alpha \cong \beta $$

$$ \gamma \cong \delta $$

Now consider the sums of the non-congruent pairs:

$$ \alpha + \gamma $$

$$ \beta + \delta $$

Since $ \gamma \cong \delta $ by assumption, we can replace one with the other in the expression $ \alpha + \gamma $:

$$ \alpha + \gamma = \alpha + \delta $$

And since $ \alpha \cong \beta $, we can make the same substitution in $ \alpha + \delta $:

$$ \alpha + \gamma = \alpha + \delta = \beta + \delta $$

It follows that the two sums have the same measure:

$$ \alpha + \gamma \cong \beta + \delta $$

Therefore, they are congruent.

Note. The same reasoning applies to subtraction: $$ \alpha - \gamma $$ $$ \beta - \delta $$ Given that $ \gamma \cong \delta $, we can write: $$ \alpha - \gamma = \alpha - \delta $$ And since $ \alpha \cong \beta $, we have: $$ \alpha - \gamma = \alpha - \delta = \beta - \delta $$ Thus, the two differences also have the same measure: $$ \alpha - \gamma \cong \beta - \delta $$

This proves that the sum (or difference) of congruent angles results in angles that are still congruent.

And so on.