Linear Pair of Angles

Linear pair of angles are two adjacent angles that share a common vertex and a side, with their other sides lying on the same straight line.

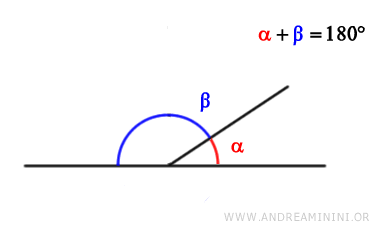
In simpler terms, two angles form a linear pair if they are adjacent and their non-shared sides form a straight line.

The sum of two angles in a linear pair is always equal to a straight angle (180° or π radians).

Thus, linear pair of angles are always supplementary angles.

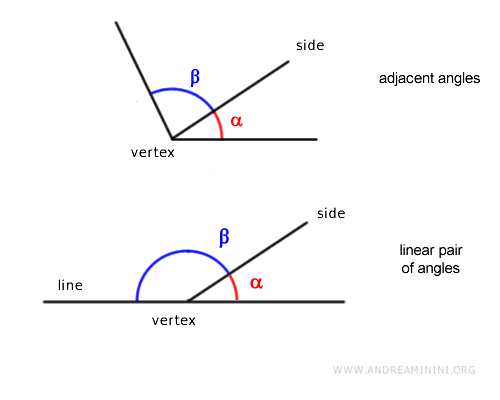
The difference between linear pairs and adjacent angles. It's important to note that all linear pairs are adjacent angles, but not all adjacent angles form a linear pair. This is because the sum of angles in a linear pair is always 180°, while the sum of two adjacent angles can vary. Both linear pairs and adjacent angles share a vertex and a side. The key feature of a linear pair is that their non-shared sides form a straight line. In contrast, adjacent angles do not necessarily align to form 180°.

A Practical Example

Consider two angles:

$$ \alpha = 60° $$

$$ \beta = 120° $$

These two angles share a common vertex and a side, with their other sides aligned on the same straight line.

Therefore, these two angles form a linear pair.

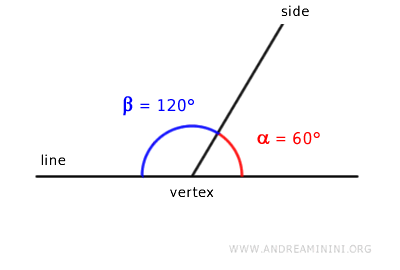
The sum of the two angles is 180°:

$$ \alpha + \beta = 180° $$

And so on.