Adding Angles

To add two consecutive angles, simply calculate the measure of the angle between the two non-common sides. $$ a \hat{O} b + b \hat{O} c = a \hat{O} c $$

When we talk about adding angles, we mean summing their measures, which can be in degrees or radians.

Example. Consider two adjacent angles, aȮb and bȮc. The non-common sides are a and c.

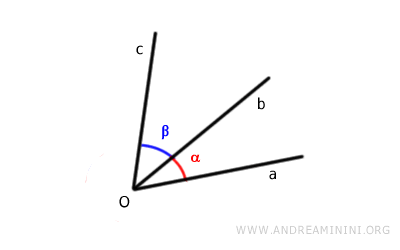
To find the sum of the angles, measure the angle between the non-common sides, that is, aȮc.

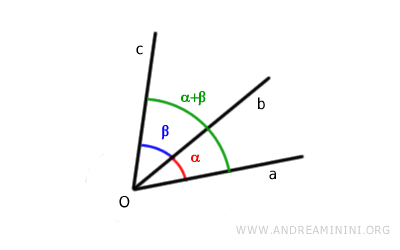
How do you add non-adjacent angles?

Geometrically, the rule for adding adjacent angles can also be applied to non-adjacent angles.

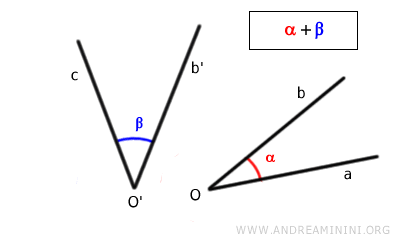
For instance, consider two non-adjacent angles.

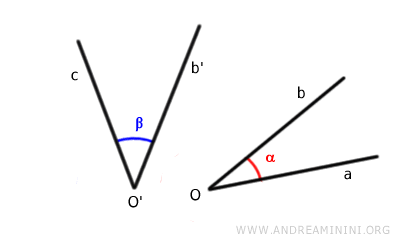
Align the vertex of the first angle with the vertex of the second angle.

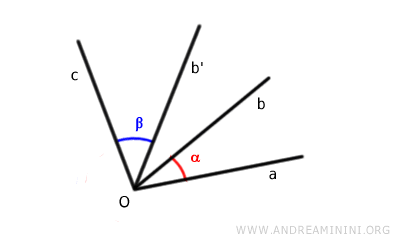
With a rigid motion, align one side of the first angle with one side of the other angle.

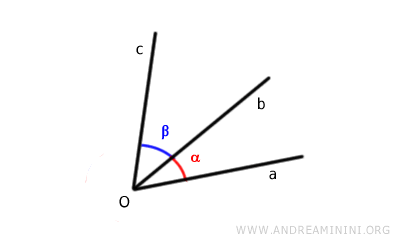
Now the two angles are adjacent and congruent to the original angles.

Therefore, you can use the same rule for adding adjacent angles. Simply measure the angle between the non-common sides.

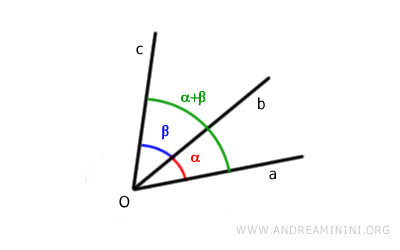
Note. Mathematically, you only need to measure the angles α and β with a protractor and add their measures (α+β), regardless of whether the angles are adjacent or not.

Properties of Angle Addition

Some properties of adding two or more angles:

• Given two pairs of congruent angles α≅β and γ≅δ, their sums are also congruent, meaning they have the same measure. $$ \alpha \cong \beta \ , \ \gamma \cong \delta \ , \ \Longrightarrow \alpha + \gamma \cong \beta + \delta $$
• Given four angles, taken in non-congruent pairs, if α>β and γ>δ, their sums will also not be congruent and will maintain the same order. $$ \alpha > \beta \ , \ \gamma > \delta \ , \ \Longrightarrow \alpha + \gamma > \beta + \delta $$

And so on.