Associated Angles in Geometry

In geometry, angles are termed "associated angles" when they are connected by a specific relationship.

Angles can be associated by their measure, their position, or in relation to two intersecting lines.

Angles Associated by Measure

Two angles are associated by measure if their sum equals a right angle or a multiple of a right angle.

Specifically, angles associated by measure are classified as:

Complementary Angles
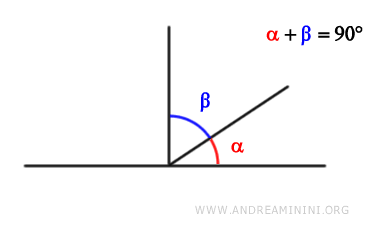
Two angles are complementary if their sum is a right angle (90° or π/2 radians).
Supplementary Angles
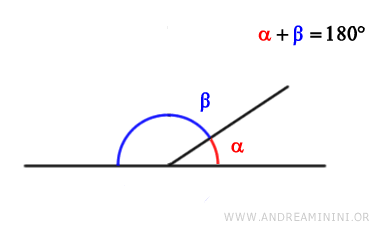
Two angles are supplementary if their sum is a straight angle (180° or π radians).
Explementary Angles
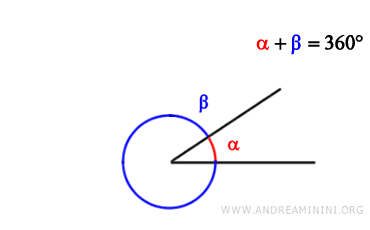
Two angles are explementary if their sum is a full angle (360° or 2π radians).

Two angles are associated by position if they share one or more sides, or their extensions.

There are several types of angles associated by position:

Consecutive Angles
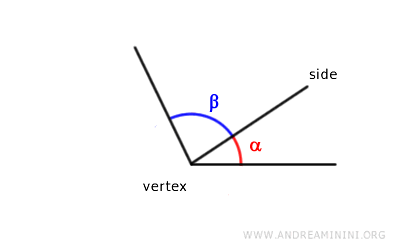
Two angles are consecutive if they share the same vertex and one side.
Adjacent Angles
Two angles are adjacent if they share the same vertex and one side, while the non-common sides lie on the same line.

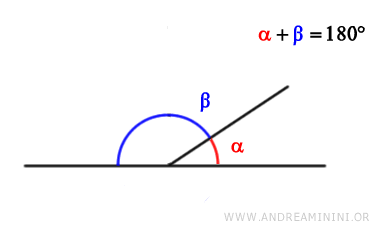
Note: In other words, adjacent angles are consecutive angles with non-common sides lying on the same line. Adjacent angles are also supplementary because their sum is always a straight angle (180°).
Vertically Opposite Angles
Two angles are vertically opposite if they are non-consecutive, share the same vertex, and the sides of one angle are the extensions of the sides of the other angle.

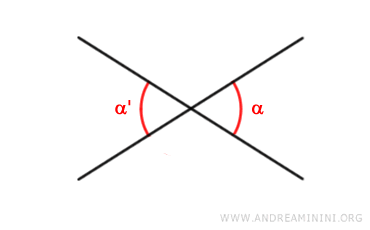
For example, angles α and α' are vertically opposite angles.

Note: Vertically opposite angles are always congruent because they have the same measure.

Consider two lines "r" and "s" intersected by a transversal line "t", forming eight angles related by specific relationships.

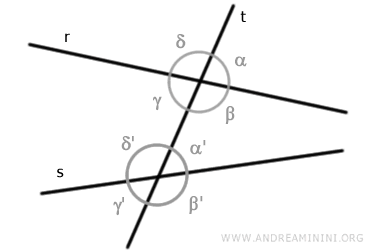
alternate, corresponding, and co-interior angles

The relationships between these associated angles are as follows:

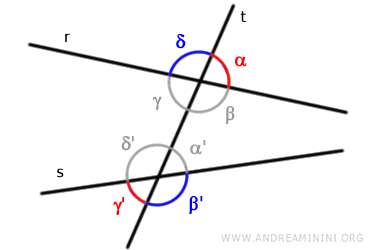
Alternate Angles
Pairs of angles that do not share a vertex and lie on opposite sides of the transversal line "t".

They are called alternate interior or alternate exterior depending on whether they lie between the two lines "r" and "s" or not. For example, the pairs of angles (γ, α') and (β, δ') are alternate interior.

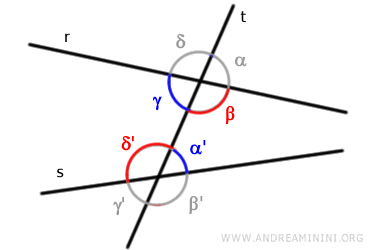
The pairs of angles (α, γ') and (δ, β') are alternate exterior.
Conjugate Angles
Pairs of angles that do not share a vertex and lie on the same side of the transversal line "t".

They are called conjugate, co-interior or co-exterior depending on whether they lie between the two lines "r" and "s" or not. For example, the pairs of angles (β, α') and (γ, δ') are co-interior.

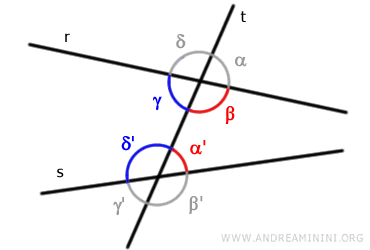
Conversely, the pairs of angles (α, β') and (δ, γ') are co-exterior.

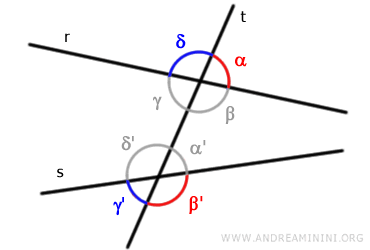
If the lines "r" and "s" are parallel, co-interior angles are also supplementary because their measures add up to a straight angle (180°).
Corresponding Angles
Pairs of angles that do not share a vertex, lie on the same side of the transversal line "t", and are positioned one inside and one outside the two lines.

For example, the pairs of angles (α, α'), (β, β'), (γ, γ'), and (δ, δ') are corresponding angles.

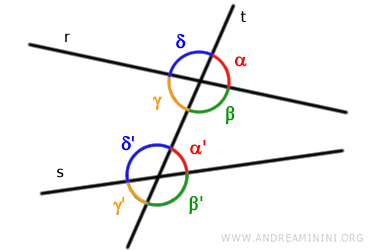
Corresponding angles have the same measure if and only if the lines "r" and "s" are parallel.