Corresponding and Opposite Sides of an Angle

In two angles with parallel sides, the sides are referred to as:

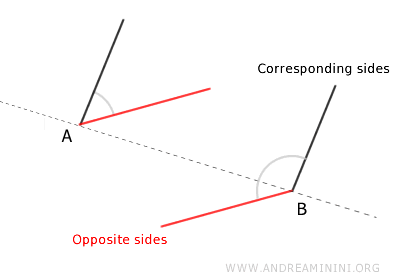
• Corresponding sides
  if they are on the same side relative to the line connecting the vertices of the two angles.
• Opposite sides
  if they are on opposite sides relative to the line connecting the vertices of the two angles.

If the parallel sides of two angles are either both corresponding or both opposite, then the angles are congruent. If not, the angles are supplementary, meaning their sum is 180°.

Explanation

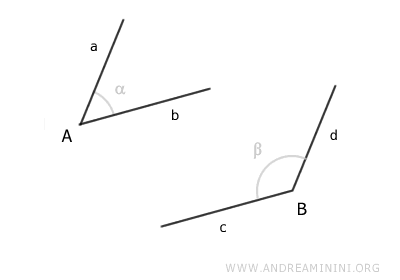
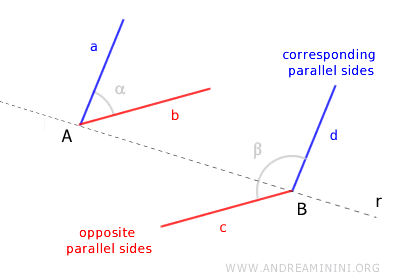
We start with two angles that have parallel sides.

Draw a line r that passes through the vertices A and B of the two angles.

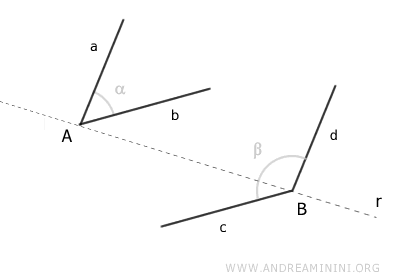
If the parallel sides of these angles are both on the same side (either left or right) of this line r, then these sides are "corresponding."

In this case, the corresponding parallel sides are sides a and d.

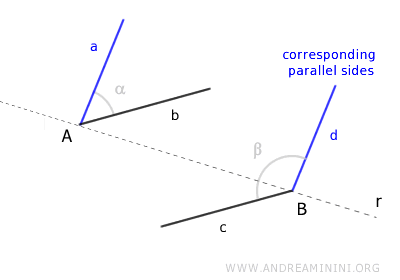
If, however, one side is on the left and the other is on the right of line r, then these parallel sides are "opposite."

In this case, the opposite parallel sides are sides b and c.

Observations

Some useful observations about corresponding and opposite sides of an angle:

• Angles with parallel sides are congruent if all their parallel sides are either corresponding or opposite.

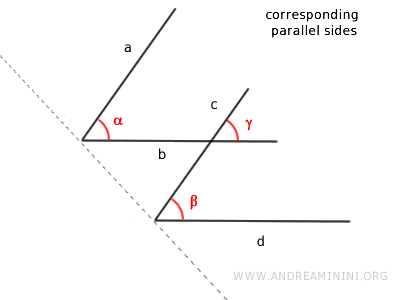
  Proof (corresponding sides). These angles have parallel sides a||c and b||d. Angles β and γ are corresponding angles of two parallel lines b and d cut by line c. Therefore, according to the parallel lines theorem, they are congruent angles β≅γ. Similarly, angles α and γ are corresponding angles of parallel lines a and c cut by line b. Hence, by the parallel lines theorem, they are congruent angles α≅γ. Finally, by the transitive property, if α≅γ and β≅γ, then angles α and β are also congruent α≅β.
  
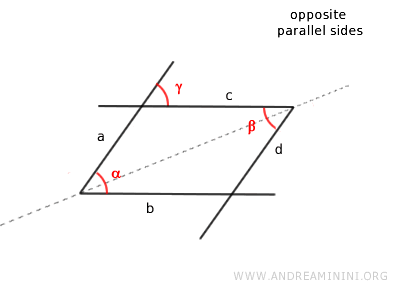
  Proof (opposite sides). These angles have parallel sides a||d and b||c. Angles β and γ are alternate interior angles of two parallel lines a and d cut by line c. Therefore, by the parallel lines theorem, they are congruent angles β≅γ. Angles α and γ are corresponding angles of parallel lines c and b cut by line a. Hence, by the parallel lines theorem, they are congruent angles α≅γ. Finally, by applying the transitive property, if α≅γ and β≅γ, then angles α and β are also congruent α≅β.
  

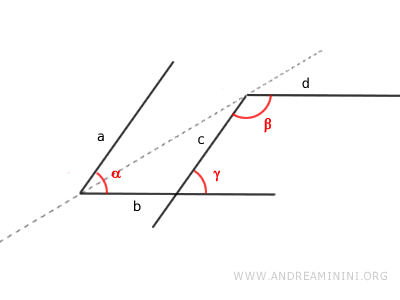
• Angles with parallel sides are supplementary if they have two corresponding sides and two opposite sides.
  

  Proof. These angles have two opposite parallel sides a||c and two corresponding parallel sides b||d. Angles β and γ are consecutive interior angles of two parallel lines b and d cut by line c. Therefore, by the parallel lines theorem, they are supplementary angles β+γ=180°. Angles α and γ are corresponding angles of parallel lines a and c cut by line b. Hence, by the parallel lines theorem, they are congruent angles α≅γ. Finally, by the transitive property, if α≅γ and β+γ=180°, then angles α and β are also supplementary α+β=180°.
  

And so on.