Angle Transport Axiom

Given a half-line originating from O' and an angle aOb originating from O, with a fixed direction of rotation, there exists a unique angle cO'd in the half-plane such that the two angles aOb and cO'd are congruent to each other. $$ aOb \ \cong \ cO'd $$

The angle transport axiom is a vital concept in Euclidean geometry because it establishes a fundamental property of angles.

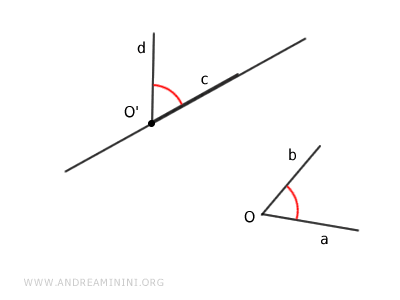
Essentially, the axiom states that angles can be transferred, or copied, from one point to another while preserving their measure.

For instance, if I take an angle and move it rigidly (e.g., through rotation, translation, etc.) without changing its measure, the new angle formed is congruent to the original one.

Note: This axiom is a consequence of the broader "Postulate of Rigid Transformations" or "Euclid's Postulate," which asserts that translations, rotations, and reflections in space can be performed without altering the measures of angles.

And so on.