Conjugate Angles
When two lines "r" and "s" are intersected by a transversal "t", two angles are termed conjugate angles if they do not share a common vertex, are both either interior or exterior, and are located on the same side of the transversal.
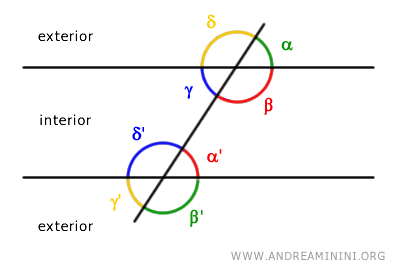
Conjugate angles can be:
- "Interior" if they are between the two lines.
- "Exterior" if they are outside the two lines.
Here’s a practical example.
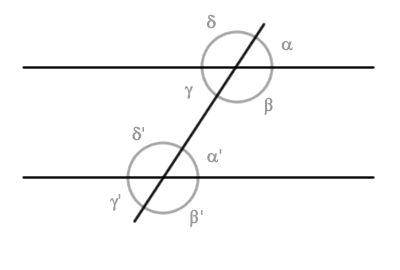
Consider two lines "r" and "s" intersected by a transversal line "t".
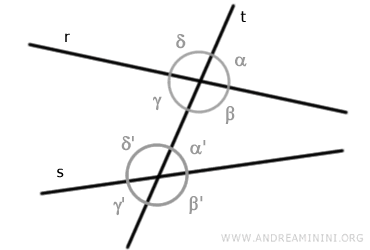
The intersection of these lines creates eight angles.
The pairs of angles (β,α') and (γ,δ') are known as interior conjugate angles.
They are called "interior" because they lie between the two lines "r" and "s".
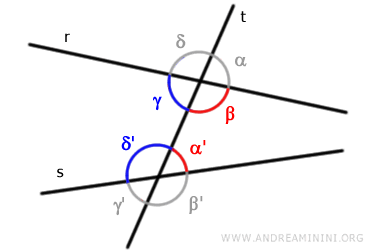
For instance, the red angles (β,α') do not share a common vertex, are both interior, and are on the same side of the transversal. The same holds true for the blue angles (γ,δ').
The pairs of angles (α,β') and (δ,γ') are known as exterior conjugate angles.
They are termed "exterior" because they lie outside the two lines "r" and "s".
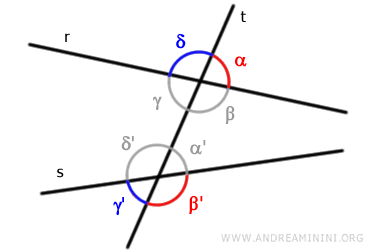
For example, the red exterior angles (α,β') do not share a common vertex, are both exterior, and are on the same side of the transversal. The same is true for the blue angles (δ,γ').
The Case of Parallel Lines
When lines "r" and "s" are parallel, the conjugate angles are also supplementary angles because their sum is equal to a straight angle (180°).
For instance, the interior conjugate angles (β,α') are also supplementary angles.
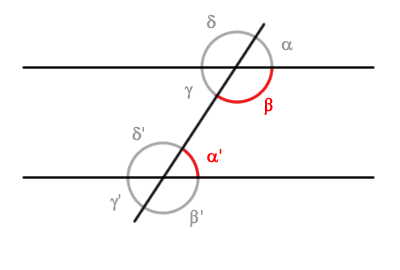
This is because angle α' is congruent with angle α, meaning they have the same measure, and angles α and β form a straight angle (180°).
The same reasoning applies to the other conjugate angles (α,β'), (δ,γ'), and (γ,δ').
