How to Measure the Arc of a Circle

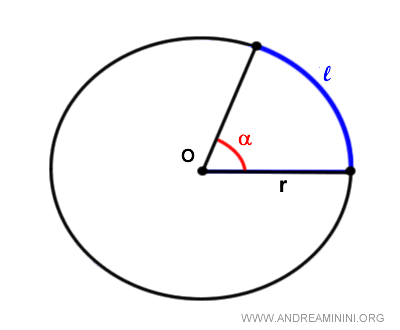
To calculate the length of a circular arc (l), multiply the angle in radians (α) by the radius of the circle (r). $$ l = \alpha \cdot r $$

Example

Let's calculate the length of a circular arc (l).

The angle is π/3 (which is 60°) and the circle has a radius of r = 5 cm.

The arc length is 5.23 cm.

$$ l = \alpha \cdot r $$ $$ l = \frac{\pi}{3} \cdot 5 \ cm $$ $$ l = \frac{3.14 \cdot 5}{3} \ cm $$ $$ l = 5.23 \ cm $$

Note: The angle must be in radians. If the angle is given in degrees (e.g., 60°), convert it to radians before applying the formula.

Proof

The proof is quite simple.

An angle measured in radians is the ratio of the arc length (l) to the radius of the circle (r):

$$ \alpha = \frac{ l }{ r } $$

With a straightforward algebraic manipulation, we find the arc length in terms of the radius and the angle:

$$ l = \alpha \cdot r $$

This demonstrates one of the practical benefits of using radians to measure angles.

And so forth.