Concave and Convex Angles

In geometry, angles can be classified based on various characteristics, including whether they are concave or convex angles.

Note: The distinction between concave and convex angles involves the position of points within the angle relative to its sides or their extensions.

Concave Angles

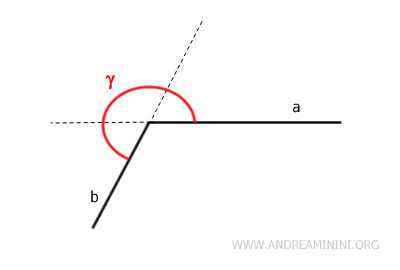
An angle is termed a concave angle if it includes the extensions of its sides within the angle.

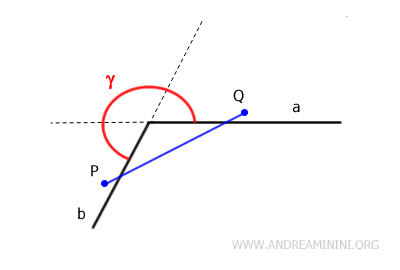
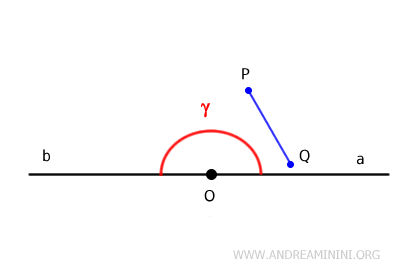
In any concave angle, you can find at least one pair of points, P and Q, within the angle such that when a segment PQ is drawn between these two points, part of this segment lies outside the angle, meaning it includes some external points.

A concave angle can be seen as an angle whose sides "bend" outward beyond 180°.

Note: It is important to note that a full angle, or a 360-degree angle, is not considered a concave angle. This is because any segment drawn between two points within the full angle is entirely contained within the angle. So, a concave angle measures more than 180° but less than 360°.

Convex Angles

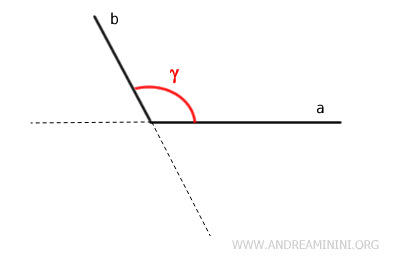
An angle is called a convex angle if it does not include the extensions of its sides within the angle.

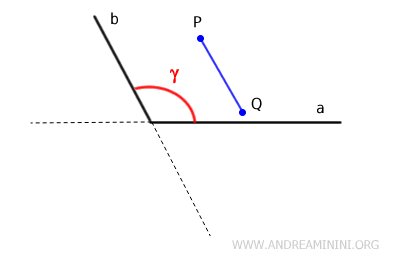
In this case, if you select any pair of points P and Q located within the angle and draw a segment connecting them, this segment PQ remains entirely within the angle.

In other words, the segment does not include any external points.

Convex angles can be seen as angles that "close" on themselves with a measure between 0 and 180°.

Note: This includes the straight angle, or a 180-degree angle. Even though a straight angle has its sides along the same line, it is still considered a convex angle because the points on the sides are not internal points of the angle. Therefore, any segment drawn between two points within the straight angle is always included within the angle and does not include any external points.

And so on.