Convex Angle

An angle is called convex if it does not include the extensions of its sides within the angle itself.

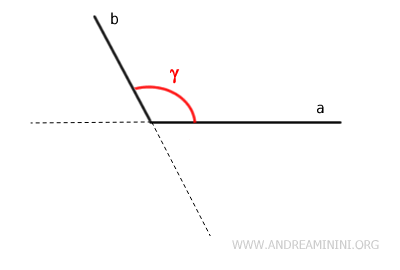
In other words, a convex angle is one that "closes" on itself with a measure greater than 0° and less than 180°.

It is different from other types of angles, such as concave angles, which measure more than 180° but less than 360°.

Convex angles include obtuse angles (between 90° and 180°), right angles (90°), and acute angles (between 0° and 90°).

Observations

Some observations about convex angles:

• In a convex angle, if you take any two internal points P and Q, the segment PQ connecting these points lies entirely within the angle. This means that segment PQ never intersects the sides of the angle and does not include points outside the angle.
  
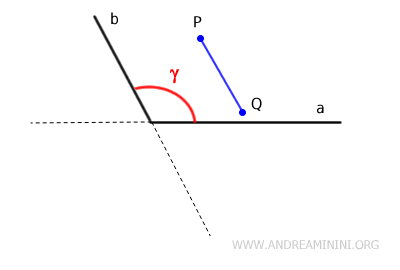
• Can a straight angle (180°) be considered convex?
  Given any two internal points P and Q, the segment PQ does not include external points, meaning it never intersects the sides of the angle. Therefore, a straight angle can be considered a convex angle.
  

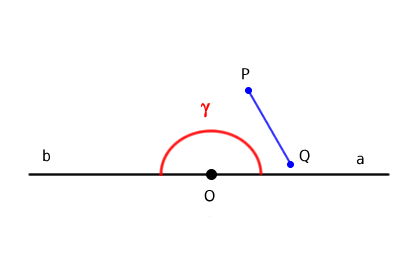
  Explanation: The points on the sides "a" and "b" of angle γ are not considered "internal points" of angle γ. Thus, if you take any two "internal" points P and Q, the segment PQ cannot intersect the sides of the angle, nor can it contain "external" points of the angle. Therefore, the straight angle meets the properties of convex angles.

  However, there are differing opinions on this matter. Some geometry texts I have read consider the straight angle convex for the reasons mentioned above. Other texts, however, classify the straight angle (180°) as neither concave nor convex because "it is not less than 180°."