Parallel Lines Theorem

Thus, to state that two lines are parallel, it is sufficient for one of these conditions to be met. If one condition is satisfied, the others will also be satisfied.

This theorem is also known as the parallelism criterion.

Note: The converse theorem also holds, meaning that if two lines are parallel, then they form pairs of congruent alternate (interior or exterior) angles, pairs of congruent corresponding angles, and pairs of supplementary conjugate (interior or exterior) angles. Therefore, the two theorems provide both necessary and sufficient conditions for the parallelism of two lines.

Proof

Given two lines r and s and a transversal, we need to determine whether r and s are parallel.

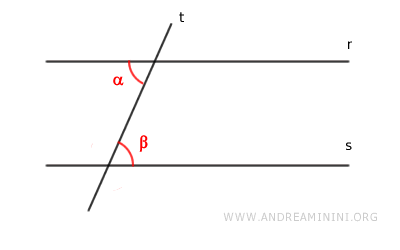
Let's start with the hypothesis that two alternate interior angles are congruent.

$$ \alpha \cong \beta $$

Then, for contradiction, assume that the two lines intersect at a point C.

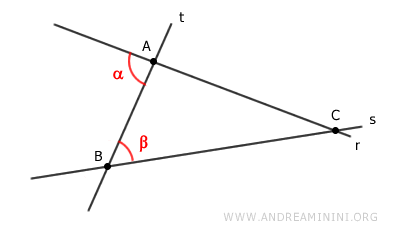
If this were true, the two lines and the transversal would form a triangle ABC.

According to the exterior angle theorem of a triangle, the exterior angle α would be greater than the non-adjacent interior angles.

Therefore, the exterior angle α is greater than the interior angle β.

$$ \alpha > \beta $$

This contradicts our initial hypothesis that α≅β, meaning the alternate interior angles are congruent.

Therefore, the statement that two lines r and s cut by a transversal with congruent alternate interior angles (α≅β) intersect at a point C is false.

If this statement is false, then its opposite must be true: two lines with congruent alternate interior angles do NOT intersect at a point C.

Knowing that if two lines do not intersect, they are parallel, we can conclude that two lines r and s cut by a transversal with congruent alternate interior angles (α≅β) are parallel lines.

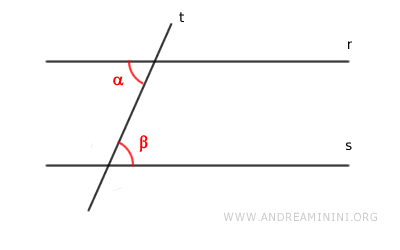
Thus, the theorem is proven for congruent alternate interior angles.

All other angle conditions can be reduced to the congruence of alternate interior angles.

• Congruent alternate exterior angles
  If the alternate exterior angles are congruent (α≅β), and knowing they are opposite to the alternate interior angles at the vertex (α≅α' and β≅β'), then the alternate interior angles are also congruent (α'≅β').
  
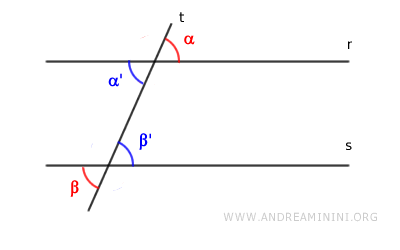
• Congruent corresponding angles
  If the corresponding angles are congruent (α≅β), and knowing that each angle is congruent to its opposite angle at the vertex (β≅β'), then the alternate interior angles are also congruent (α≅β').
  
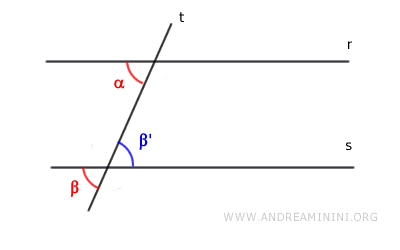
• Supplementary conjugate angles
  If the conjugate angles are supplementary (α+β=180°), and knowing that the adjacent angles on lines r and s are also supplementary (α+β'=180°), then the alternate interior angles are congruent (α≅β').
  

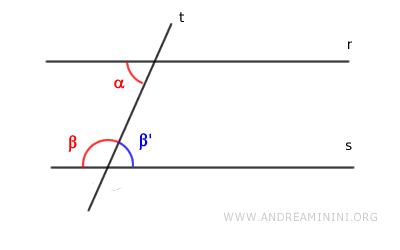
Once the problem is reduced to the case of congruent alternate interior angles, nothing more needs to be done as the theorem has already been proven.

The Converse Parallel Lines Theorem

Proof

In this case, the initial hypothesis is that two lines are parallel.

$$ r // s $$

We need to prove that there exist two congruent alternate interior angles α≅β.

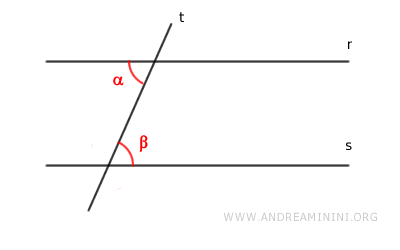
Again, we use a proof by contradiction.

We start with the hypothesis that two parallel lines have non-congruent alternate interior angles, for instance, α>β.

$$ \alpha > \beta $$

The situation would then look like this.

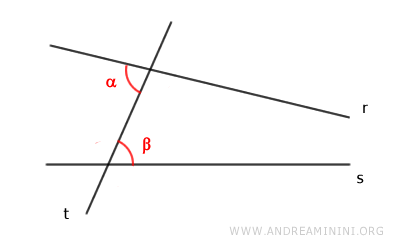
Thus, we could draw another line r' that has an alternate interior angle α' congruent with β, i.e., α'≅β.

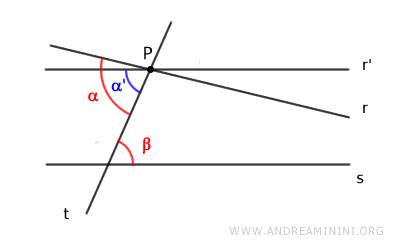
However, this would result in two lines parallel to s passing through point P.

• The lines r // s are parallel by the initial hypothesis
• The lines r' // s are parallel by the parallel lines theorem because they have a pair of congruent alternate angles α'≅β

The existence of two lines parallel to line s passing through the same point P contradicts the parallel postulate.

According to the parallel postulate, there can be only one line parallel to s passing through point P.

Therefore, the statement that two parallel lines r and s have non-congruent alternate interior angles is false.

Consequently, the opposite statement is true: two parallel lines r and s have congruent alternate interior angles (α≅β).

This proves the theorem for congruent alternate interior angles.

Similarly, all other cases (e.g., congruent alternate exterior angles, congruent corresponding angles, supplementary conjugate interior/exterior angles) can be reduced to the case of congruent alternate interior angles. Therefore, this proof applies to all scenarios.

Remarks

Some remarks on the parallel lines theorem:

• Corollary < p class="definition">If two lines, r and s, are both perpendicular to a third line t, then they are parallel to each other.
  

   

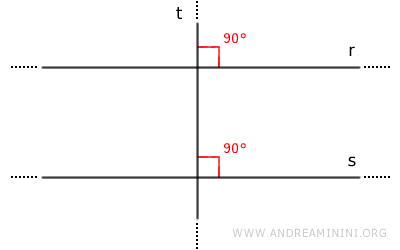
  This is because when two lines are perpendicular to the same line, they create corresponding angles of 90° that are congruent. According to the parallel lines theorem, this implies that the two lines are parallel.

  Note: Similarly, it can be observed that lines r and s form pairs of congruent alternate (interior or exterior) angles or pairs of supplementary conjugate angles (180°). In any case, the logical deduction is that lines r and s are parallel.

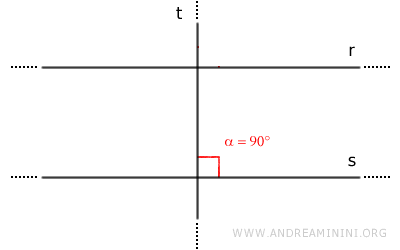
• Given two parallel lines r and s, if a line t is perpendicular to one of them, it is also perpendicular to the other.
  

  Proof: Consider two parallel lines r // s and a third line t perpendicular to line s. Lines t and s form a right angle α=90°.
  
  Since r and s are parallel, according to the parallel lines theorem, lines r and s form pairs of congruent corresponding angles with a transversal. Thus, angle β is also a right angle (β=90°).
  
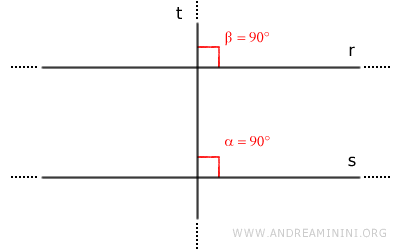
  Consequently, line t is also perpendicular to line r.

And so on.