Perpendicular Lines
Two intersecting lines are called perpendicular lines when they divide the plane into four right angles (90°).
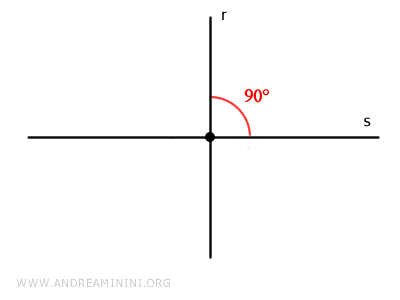
To indicate that two lines are perpendicular, we use the upside-down T symbol: $$ r \perp s $$
Let's consider two distinct lines, r and s, on a plane.
These lines are intersecting lines because they cross at a single point P, known as the "foot of the perpendicular".
The intersection of the two lines divides the Cartesian plane into four sections and four angles.
If one angle is a right angle (90°), then all the other angles are also right angles.
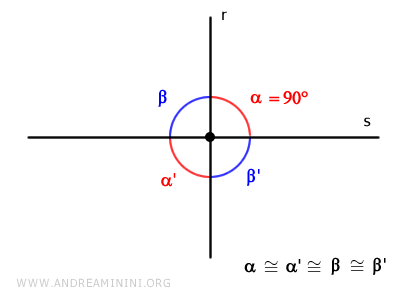
In this case, the two lines are perpendicular to each other.
Explanation: For intersecting lines, opposite vertical angles are congruent α≅α' and β ≅β'. $$ \alpha \cong \alpha ' $$ $$ \beta \cong \beta ' $$ Thus, if one angle is a right angle α=90°, the opposite angle α'=90° is also a right angle, since they are congruent α≅α' $$ \alpha = \alpha ' = 90° $$ Their sum is α+α'= 180°. $$ \alpha + \alpha' = 90° + 90° = 180° $$ Knowing that the sum of the angles is 360°, the sum of the remaining angles β+β' must also be 180° $$ \alpha + \alpha ' + \beta + \beta ' = 360° $$ $$ \beta + \beta ' = 360° - ( \alpha + \alpha' ) = 360° - 180° = 180° $$ Angles β and β' are congruent (β≅β') because they are opposite vertical angles. Therefore, each has a measure of 90°. $$ \beta = \beta ' = \frac{180°}{2} = 90° $$ Hence, all angles are congruent, each measuring 360°/4 = 90°.
Given a line r and a point P that is not on the line, there is exactly one line passing through point P that is perpendicular to line r.
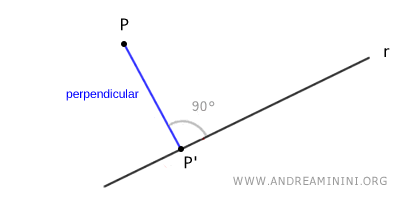
A line that intersects another line without being perpendicular to it is referred to as an "oblique line".
How can you verify if two lines are perpendicular?
In analytic geometry, two lines $ y=mx+q $ and $ y=m'x+q' $ are perpendicular if the product of their slopes equals -1:
$$ m \cdot m' = -1 $$
Alternatively, if the equations are in implicit form, two lines $ ax+by+c=0 $ and $ a'x+b'y+c'=0 $ are perpendicular if they satisfy the perpendicularity condition:
$$ aa'+ bb' = 0 $$
This condition can also be applied if the lines are parallel to the Cartesian axes.
In any case, both conditions are valid for verifying the perpendicularity of lines and can be used depending on the form of the equations: $$ r \perp s \ \Longleftrightarrow \ m \cdot m' = -1 \ \Longleftrightarrow \ aa'+bb'= 0 $$
The Slopes of Perpendicular Lines
Two lines are perpendicular if and only if the product of their slopes, m and m', is equal to -1: $$ m \cdot m' = -1 $$ that is, $$ m = - \frac{1}{m'} $$
Two lines y=mx+q and y=m'x+q' are perpendicular lines if they intersect at a point forming a 90° angle.
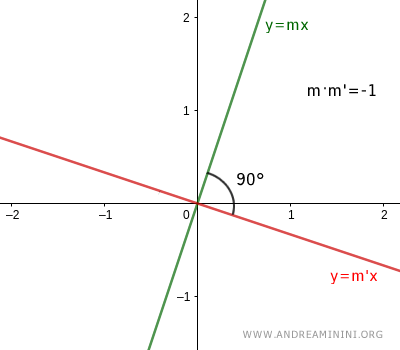
When two lines are perpendicular, the product of their slopes is equal to -1:
$$ m \cdot m' = -1 $$
Therefore, the slopes of two perpendicular lines are each other's negative reciprocal:
$$ m = - \frac{1}{m'} $$
This theorem applies only if neither line is parallel to the axes.
Note: If one of the lines is parallel to the x-axis, its slope is zero (m=0), and the negative reciprocal -1/m would be a division by zero. If one of the lines is parallel to the y-axis, its slope cannot be calculated using the formula m=y/x. Therefore, in both cases, the theorem is not applicable.
The reverse argument also holds true.
Two lines with slopes such that m·m'=-1 are perpendicular lines.
Practical Example
Consider two perpendicular lines:
$$ r = 2x $$
$$ r'= -\frac{1}{2} x $$
The two lines intersect at the origin, forming a 90° angle.
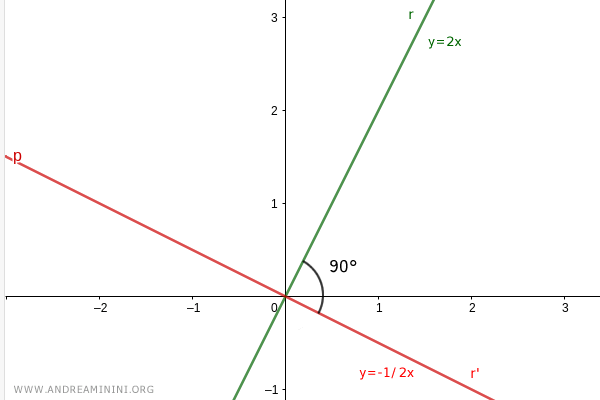
The slopes of the two lines are negative reciprocals of each other:
$$ m=2 $$
$$ m' = - \frac{1}{2} $$
Example 2
Consider two lines with negative reciprocal slopes:
$$ r = 3x $$
$$ r'= -\frac{1}{3} x $$
Let's plot the lines on the plane.
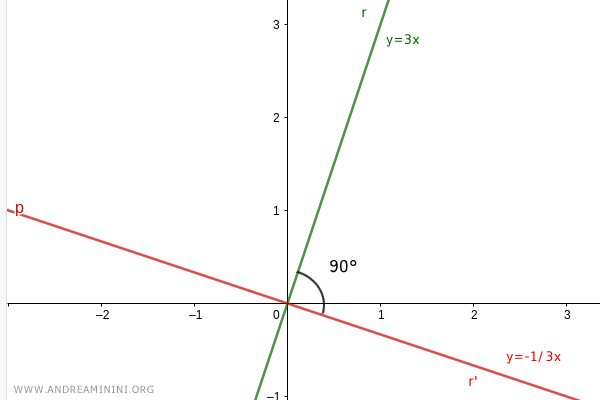
The angle between the two lines is a right angle.
Therefore, the two lines are perpendicular.
Proof
Consider two perpendicular lines, r and r', that are not parallel to the Cartesian axes:
$$ r: \ y=mx+q $$ $$ r': \ y=m'x+q' $$
Since the lines are perpendicular, they intersect at a point forming four 90° angles.
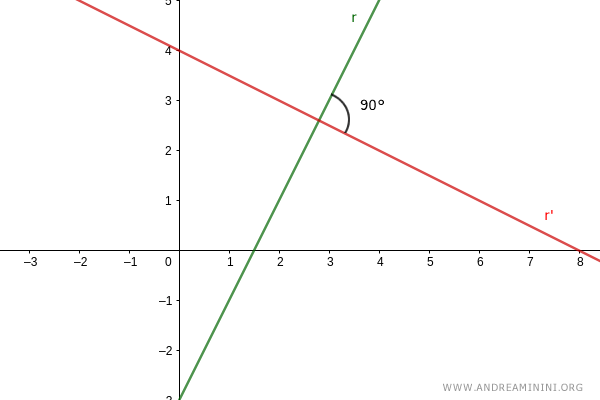
To simplify calculations, consider the parallel lines to r and r' that pass through the origin (q=0 and q'=0).
Since they are parallel, they have the same slopes, m and m', as the original lines.
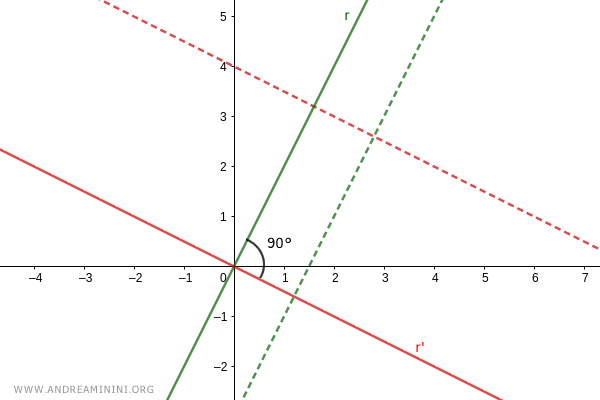
Consider a point A=(xA;yA) on line r with xA=1.
Its projection on the x-axis is a segment of length AB.
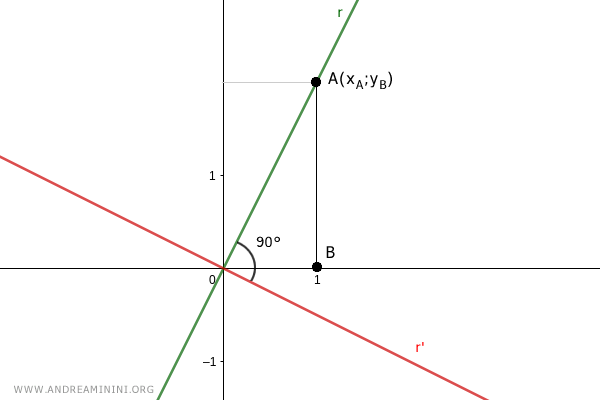
Consider a point C on the x-axis that is the same distance from the origin as OC=AB.
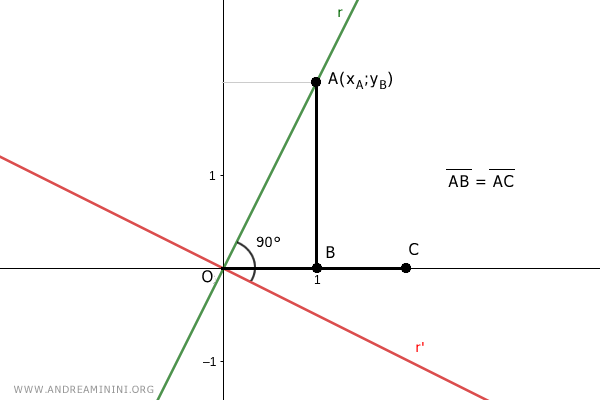
Draw a perpendicular from point C to intersect point D=(xD;yD) on line r'.
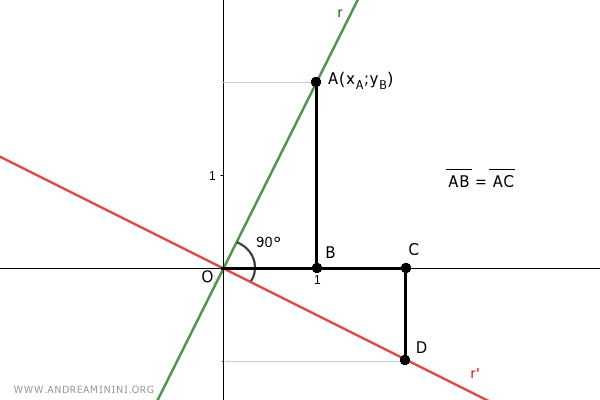
The two right triangles, OAB and OCD, share a side, AB=OC, because they are constructed that way.
Being right triangles, they both have a right angle.
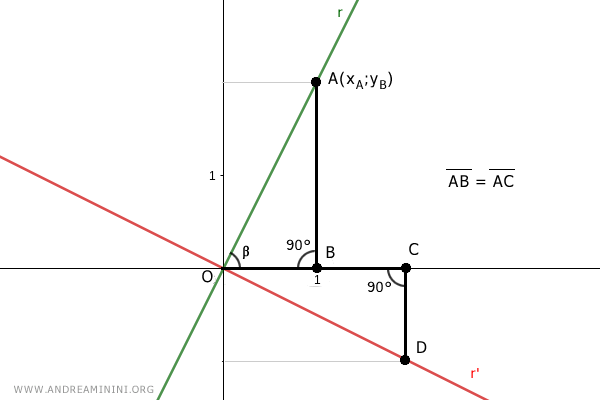
Additionally, the two triangles have angles α and α' that are complementary to angle β.
Thus, α=α' have the same measure.
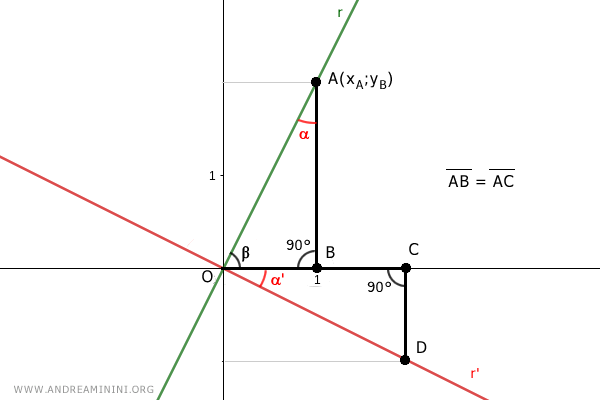
As right triangles, the sum of their angles is 180°. Therefore, the third angle of both triangles is also equal.
The two triangles, OAB and OCD, are congruent because they have congruent angles and one congruent side, AB≅OC.
Therefore, the two triangles have the same sides. Particularly, it's useful to know that OA=OC:
$$ \overline{OA} = {CD} $$
Knowing that OA=1 by construction, CD=1 as well.
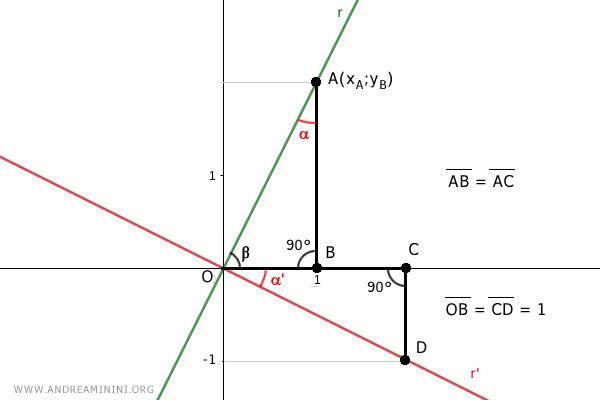
If segment CD=1, then point D is located at coordinates D(xD,-1).
So, the coordinates of points A and D are:
$$ A=(1;y_A) $$
$$ D=(x_D;-1) $$
Using the coordinates of the two points (xA;yA)=(1;yA) and (xD;yD)=(xD;-1), we can calculate the slopes of the two lines r and r':
$$ m = \frac{y_A}{x_A} = \frac{y_A}{1} = y_A $$
$$ m' = \frac{y_D}{x_D} = \frac{-1}{x_D} $$
Knowing that AB=OC from the initial assumption, yA=xD.
Thus, the two slopes are each other's negative reciprocal:
$$ m = y_A $$
$$ m' = - \frac{1}{y_A} $$
Alternative Proof
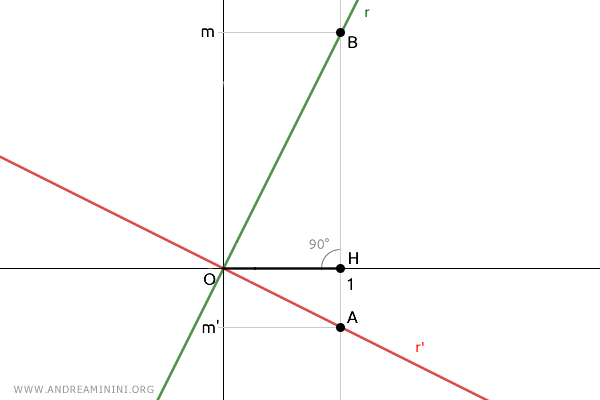
Assume two perpendicular lines, r and r', passing through the origin of the plane, O.
Draw a unit segment, OH=1, on the positive x-axis.
Then, draw a line perpendicular to the x-axis passing through point H at coordinates (1;0) on the plane.
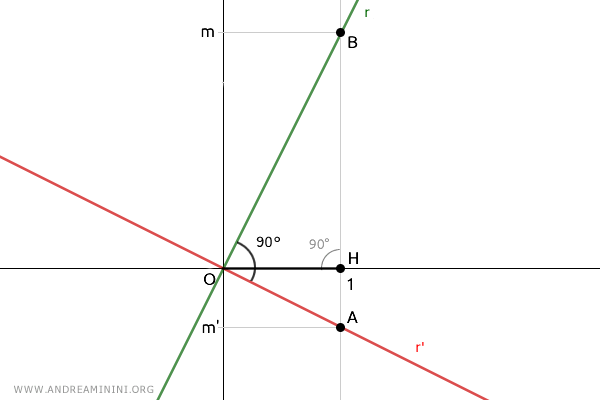
This allows us to find the slopes of the two lines:
$$ m = \frac{ \overline{BH}}{ \overline{OH}} $$
$$ m' = \frac{ \overline{AH}}{ \overline{OH}} $$
Since OH=1 by construction:
$$ m = \frac{ \overline{BH}}{ \overline{OH}} = \frac{ \overline{BH}}{1} = \overline{BH} $$
$$ m' = \frac{ \overline{AH}}{ \overline{OH}} = \frac{ \overline{AH}}{1} = \overline{AH} $$
So, the slopes, m and m', are equal to the lengths of segments $ \overline{BH} $ and $ \overline{AH} $.
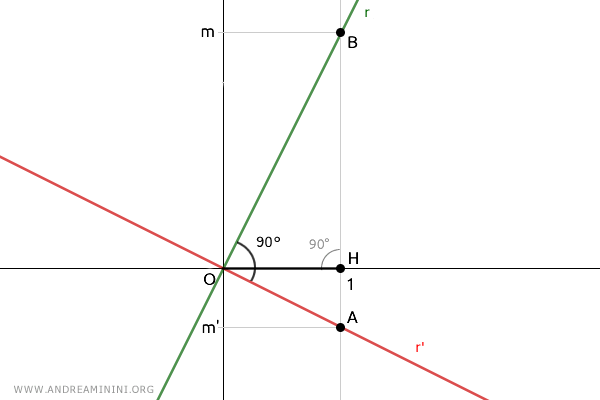
The triangle OAB is a right triangle because OA and OB lie on lines r' and r, respectively, which are perpendicular to each other by initial assumption, thus forming a 90° angle.
Additionally, segment OH is the height of triangle OAB by construction, as it is perpendicular to the side AB of the triangle.
According to the second theorem of Euclid, the square of the height relative to the hypotenuse $ \overline{OH}^2 $ is equal to the product of the projections of the legs on the hypotenuse $ \overline{AH} \cdot \overline{BH} $:
$$ \overline(OH)^2 = \overline{AH} \cdot \overline{BH} $$
Knowing that OH=1:
$$ 1^2 = \overline{AH} \cdot \overline{BH} $$
$$ 1 = \overline{AH} \cdot \overline{BH} $$
Additionally, knowing that AH=|m| and BH=|m'|:
$$ 1 = | m | \cdot |m'| $$
Thus, the product of the absolute values of the slopes m and m' equals 1.
Since the lines are perpendicular to each other, the product of their slopes is negative.
It is evident from the graph that m and m' have opposite signs.
In this case, m lies on the positive y-axis and is positive (m>0), while m' lies on the negative y-axis (m<0).
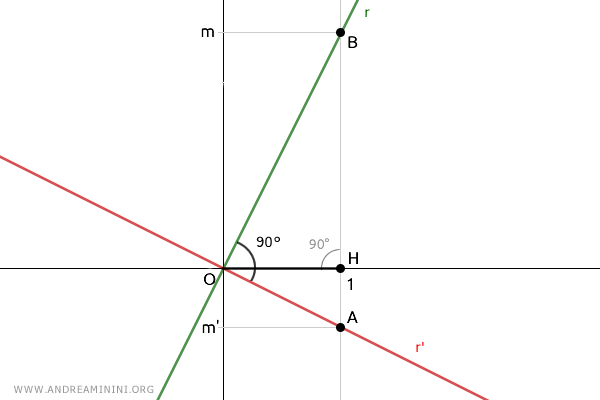
Therefore, removing the absolute value from m and m', the product of the slopes is -1:
$$ -1 = m \cdot m' $$
This concludes the proof.
Note: This proof also applies if the perpendicular lines, s and s', do not pass through the origin: $$ s: \ y = mx+q $$ $$ s': \ y = m'x+q' $$ because we can simply find their parallel lines, s||r and s'||r', that pass through the origin (0,0): $$ r: \ y = mx $$ $$ r': \ y = m'x $$ If s and s' are perpendicular, then their parallel lines, r and r', are also perpendicular.
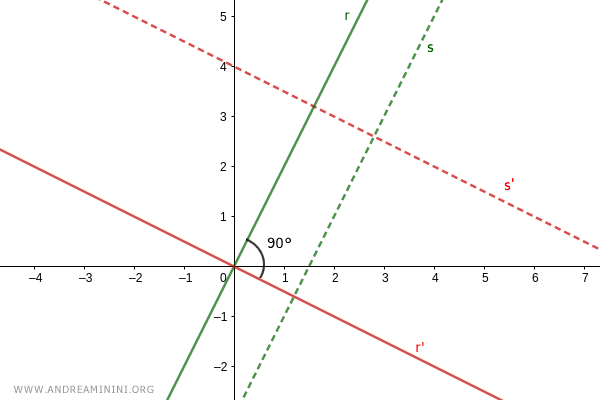
Reverse Proof
In this case, the initial assumption is that the product of the slopes of two lines equals -1:
$$ m \cdot m' = -1 $$
Draw a segment, OH=1, and construct the triangle OAB:
To prove that lines r and r' are perpendicular, we apply the inverse of Euclid's second theorem:
If in a triangle the square of the height is equal to the product of the lengths of the two segments into which the opposite side is divided by the height, then the triangle is a right triangle and the vertex (C) from which the height originates is a right angle (90°).
$$ \overline{OH}^2 = \overline{AH} \cdot \overline{BH} $$
In this case, AH=|m'| and BH=|m|, where the slopes are in absolute value because we are measuring the lengths of segments AH and BH:
$$ \overline{OH}^2| = |- \frac{1}{m}| \cdot |m| $$
$$ \overline{OH}^2| = 1 $$
Since OH=1 by construction, the equation is satisfied.
Thus, according to the inverse of Euclid's second theorem, the angle from which height OH originates is a right angle (90°) and the triangle OAB is a right triangle.
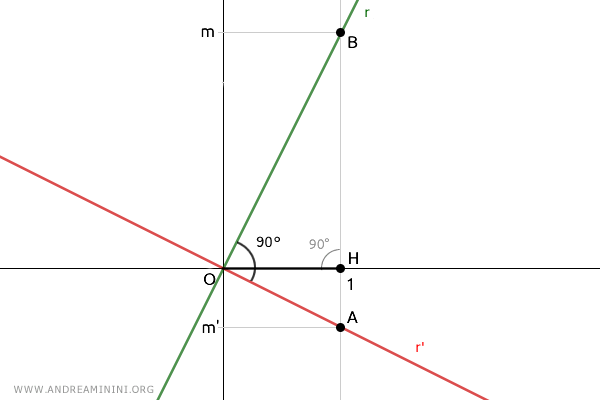
If OA and OB are two perpendicular segments (90°), then the lines r' and r in which they lie are also perpendicular.
This proves that the two lines, r and r', are perpendicular to each other.
The Perpendicularity Condition
Two lines $ ax+by+c=0 $ and $ a'x+b'y+c'=0 $ are perpendicular if they satisfy the perpendicularity condition: $$ aa' + bb' = 0 $$
One advantage of this condition is that it can be used to verify perpendicularity even when the lines are parallel to the Cartesian axes.
Example
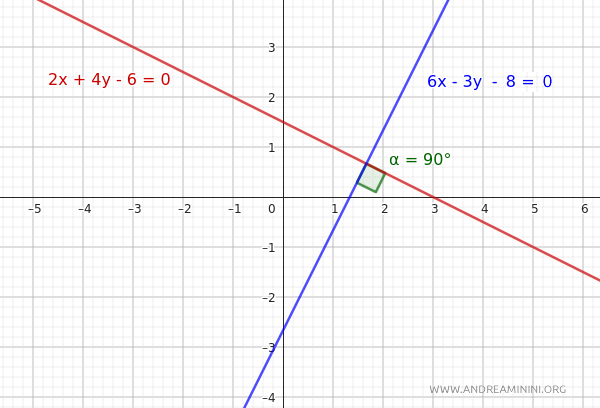
Consider two lines with equations in implicit form:
$$ r: 2x+4y-6=0 $$
$$ r': 6x-3y-8=0 $$
To check if they are perpendicular, use the perpendicularity condition:
$$ aa'+bb'=0 $$
In this case, the coefficients of the first line are a=2, b=4, while those of the second line are a'=6 and b'=-3:
$$ 2 \cdot 6 + 4 \cdot (-3)=0 $$
$$ 12 -12 =0 $$
$$ 0 =0 $$
The condition is satisfied, so the two lines, r and r', are perpendicular.
Note: To quickly check if two lines are perpendicular without looking at the graph, write their equations in implicit form one below the other, aligning the x and y variables in columns, and mentally calculate the algebraic sum of the products of the two columns A and B. If the result is zero, the lines are perpendicular.
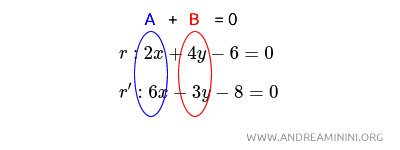
For example, in this case, A=2·6 and B=4·(-3), that is A=12 and B=-12. The algebraic sum of the products is A+B=12+(-12)=0. The result is zero, so the two lines are perpendicular.
Proof
Consider two lines, r and s, in implicit form:
$$ ax+by+c=0 $$
$$ a'x+b'y+c'=0 $$
The slopes of the two lines are:
$$ m = - \frac{a}{b} $$
$$ m' = - \frac{a'}{b'} $$
When two lines are perpendicular, the product of their slopes is equal to -1:
$$ m \cdot m' = -1 $$
$$ m = \frac{-1}{m'} $$
Substitute m=-a/b and m=-a'/b':
$$ - \frac{a}{b} = \frac{-1}{[ - \frac{a'}{b'} ]} $$
$$ - \frac{a}{b} = \frac{1}{\frac{a'}{b'}} $$
$$ - \frac{a}{b} = \frac{b'}{a'} $$
$$ - aa' = bb' $$
$$ - aa' - bb' = 0 $$
$$ (- aa' - bb') \cdot (-1) = 0 \cdot (-1) $$
$$ aa' + bb' = 0 $$
The perpendicularity condition is proven.
Line Perpendicular to a Plane
A line \( r \) is said to be perpendicular to a plane \( \alpha \) if it intersects the plane and is perpendicular to every line that lies within the plane.
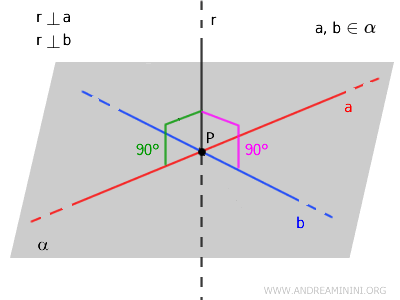
In simpler terms, a line is perpendicular to a plane \( \alpha \) if it meets the following two criteria:
- The line \( r \) intersects the plane \( \alpha \) at exactly one point, meaning it is "incident to the plane."
- The line \( r \) is perpendicular to all lines within the plane \( \alpha \) that pass through the intersection point.
This is equivalent to saying that the direction vector of the line \( r \) is "parallel to the normal vector" of the plane \( \alpha \).
A line that intersects a plane without being perpendicular to it is referred to as an oblique line.
Observations
Additional notes and observations on perpendicular lines:
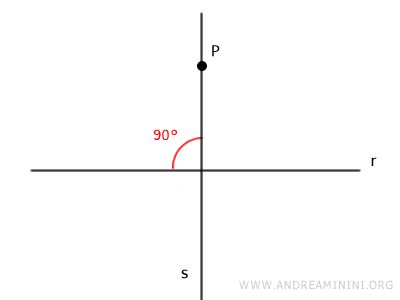
- Perpendicular Theorem
Given a point P and a line r on the plane, there is one and only one line s passing through point P and perpendicular to line r.
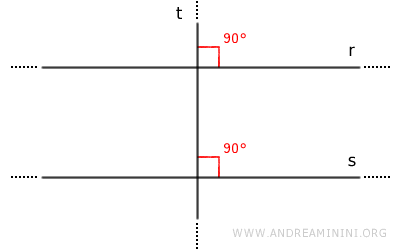
- Two lines r and s perpendicular to a third line t are parallel
Lines r and s form pairs of corresponding congruent angles. Therefore, by the parallel lines theorem, they are parallel.
- A line t perpendicular to line r is also perpendicular to all lines parallel to line r
Given two parallel lines r and s, if line t is perpendicular to one of the lines r or s, it is also perpendicular to the other line.
Proof: Assume two parallel lines r//s and a third line t perpendicular to line s. Thus, lines t and s form a right angle (α=90°).
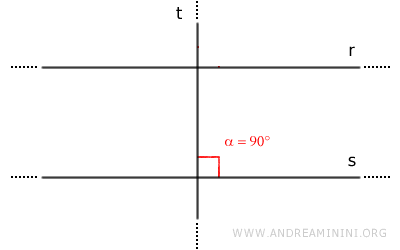
Since lines r and s are parallel (r//s), by the parallel lines theorem, lines r and s form pairs of corresponding congruent angles with the same transversal line (α≅β). Therefore, angle β is also a right angle (β=90°).
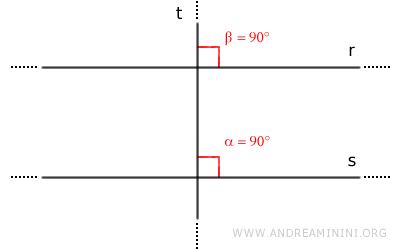
Consequently, line t is also perpendicular to line r. - The perpendiculars of two intersecting lines are also intersecting lines
Given two intersecting lines r and s, their respective perpendiculars p and q are intersecting lines.
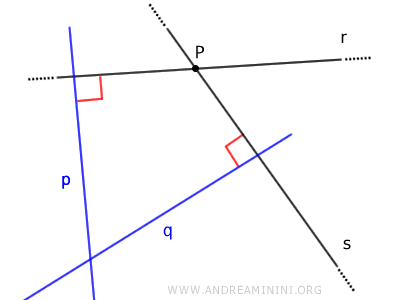
Proof: This statement is proven by contradiction. Assume two intersecting lines r and s with respective parallel perpendiculars p // q. Since p and q are parallel lines, by the parallel lines theorem, the corresponding interior angles α and β with a transversal line t should be supplementary, meaning their sum should be a straight angle (α+β=180°).
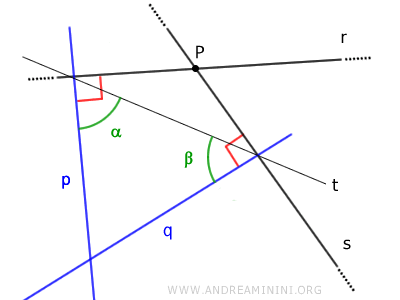
In reality, angles α and β are both acute angles as they cut the right angle (90°). Therefore, their sum is less than 180° and lines p and q are not parallel. This contradicts the initial assumption. Consequently, the thesis that two intersecting lines r and s have parallel perpendiculars p//q is false. Thus, the negation is true, which means "two intersecting lines r and s have intersecting perpendiculars" as the sum of the conjugate angles alpha plus beta is less than 180°.
And so on
