How to Determine if Two Lines Are Intersecting, Parallel, or Coincident
To determine the relationship between two lines in the Cartesian plane $$ r: ax + by + c = 0 $$ and $$ r': a'x + b'y + c' = 0 $$ we examine their general form equations and compare their coefficients and constants.
- Intersecting Lines
If the ratio of the coefficients is not proportional, the two lines intersect at a single point. $$ \frac{a}{a'} \ne \frac{b}{b'} $$ - Parallel and Distinct Lines
If the ratio of the coefficients is proportional but the ratio of the constants is different, the two lines are parallel and distinct, meaning they never intersect. $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$ - Coincident Lines
If the ratio of the coefficients is proportional and equal to the ratio of the constants, the two lines are coincident, meaning they overlap completely. $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$
Note: These formulas are derived directly from the criteria for parallelism $$ \frac{a}{a'} = \frac{b}{b'} $$ and coincidence of lines $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$
A Practical Example
Consider two lines with the following equations:
$$ r: 2x + 3y + 4 = 0 $$
$$ r': 4x + 6y + 12 = 0 $$
First, let's check if they satisfy the parallelism criterion by analyzing the ratio of the coefficients a=2, b=3 and a'=4, b'=6 in the equations.
$$ \frac{a}{a'} = \frac{2}{4} = \frac{1}{2} $$
$$ \frac{b}{b'} = \frac{3}{6} = \frac{1}{2} $$
The ratio of the coefficients is proportional, so the lines are not intersecting.
$$ \frac{a}{a'} = \frac{b}{b'} = \frac{1}{2} $$
This means the lines are parallel, but it’s not yet clear if they are distinct or coincident.
To determine this, we check if the lines satisfy the coincidence criterion by analyzing the ratio of the constants c=4 and c'=12.
$$ \frac{c}{c'} = \frac{4}{12} = \frac{1}{3} $$
The ratio of the constants is not equal to the ratio of the coefficients, so the lines do not satisfy the coincidence criterion.
$$ \frac{c}{c'} = \frac{1}{3} \ne \frac{1}{2} = \frac{a}{a'} = \frac{b}{b'} $$
This means the lines are not coincident.
Thus, by elimination, the two lines are distinct and parallel.
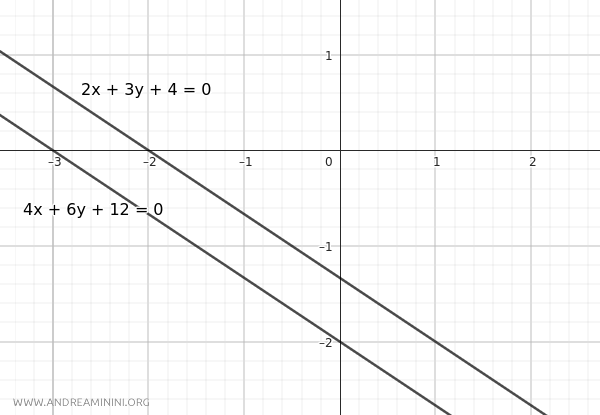
Example 2
In this example, let's consider the following lines:
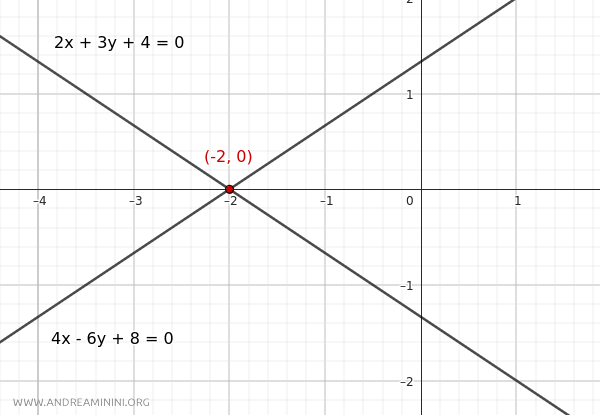
$$ r: 2x + 3y + 4 = 0 $$
$$ r': 4x - 6y + 8 = 0 $$
To determine if they are intersecting or parallel, we check if they satisfy the parallelism condition.
$$ \frac{a}{a'} = \frac{2}{4} = \frac{1}{2} $$
$$ \frac{b}{b'} = \frac{3}{-6} = -\frac{1}{2} $$
In this case, the parallelism condition $$ \frac{a}{a'} = \frac{b}{b'} $$ is not satisfied.
$$ \frac{1}{2} \ne -\frac{1}{2} $$
Therefore, the two lines are intersecting. They meet at a single point.
What is the intersection point of the intersecting lines?
To find it, we solve the following system of linear equations:
$$ \begin{cases} 2x + 3y + 4 = 0 \\ 4x - 6y + 8 = 0 \end{cases} $$
We solve the system using the substitution method. Any other method would also work.
For example, we solve for x in the first equation and substitute it into the second equation.
$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ 4x - 6y + 8 = 0 \end{cases} $$
$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ 4 \cdot \left( \frac{-4 - 3y}{2} \right) - 6y + 8 = 0 \end{cases} $$
$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ \frac{-16 - 12y}{2} - 6y + 8 = 0 \end{cases} $$
$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ \frac{-16 - 12y - 12y + 16}{2} = 0 \end{cases} $$
$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ \frac{-24y}{2} = 0 \end{cases} $$
$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ -12y = 0 \end{cases} $$
$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ -12y \cdot \left( -\frac{1}{12} \right) = 0 \cdot \left( -\frac{1}{12} \right) \end{cases} $$
$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ y = 0 \end{cases} $$
Once we find y=0 from the second equation, we substitute it into the first equation.
$$ \begin{cases} x = \frac{-4 - 3 \cdot 0}{2} \\ y = 0 \end{cases} $$
$$ \begin{cases} x = \frac{-4}{2} \\ y = 0 \end{cases} $$
$$ \begin{cases} x = -2 \\ y = 0 \end{cases} $$
The solution to the system is x=-2 and y=0.
Thus, the intersecting lines meet at the point (x,y)=(-2,0) in the Cartesian plane.
Calculating the Determinant
An alternative and often more straightforward method to determine the relationship between two lines is by calculating the determinant formed by the coefficients of the variables \(x\) and \(y\).
$$ D = a \cdot b' - b \cdot a' $$
Where a, a', b, and b' are the coefficients of the variables x and y in the general form equations of the two lines.
$$ r: ax + by + c = 0 $$
$$ r': a'x + b'y + c' = 0 $$
Depending on the value of the determinant, the two lines either intersect or do not intersect:
- \(D \neq 0\)
If the determinant is non-zero, the lines intersect at one point. - \(D = 0\)
If the determinant is zero, the lines do not intersect. They may be parallel and distinct or coincident.
When the determinant is zero \(D = 0\), the lines satisfy the parallelism criterion.
$$ \frac{a}{a'} = \frac{b}{b'} $$
We then need to determine if they also satisfy the coincidence criterion.
In this case, we calculate the ratio of the constants and check if \( \frac{c}{c'} \) is equal to \( \frac{a}{a'} \) and \( \frac{b}{b'} \).
- If \( \frac{c}{c'} = \frac{a}{a'} = \frac{b}{b'} \), the lines are coincident and share all points.
- If the ratio \(\frac{c}{c'}\) is different or if one of the ratios does not exist (because the denominator is zero while the numerator is not), the lines are parallel and distinct.
Example
Consider the following lines:
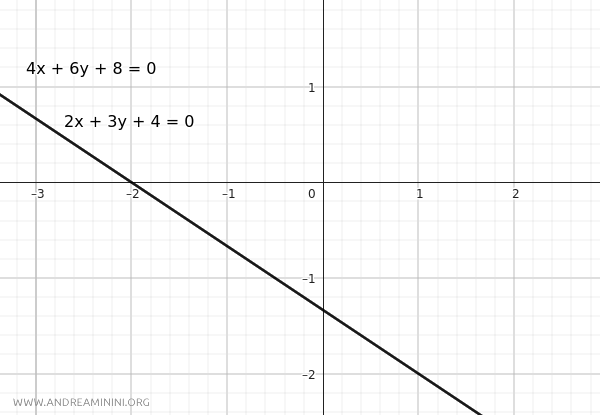
$$ r: 2x + 3y + 4 = 0 $$
$$ r': 4x + 6y + 8 = 0 $$
Calculate the determinant:
$$ D = 2 \times 6 - 3 \times 4 = 12 - 12 = 0 $$
Since \(D = 0\), the lines do not intersect. Therefore, they are parallel.
Now, let's check if they are coincident or distinct.
$$ \frac{2}{4} = \frac{3}{6} = \frac{4}{8} = \frac{1}{2} $$
All ratios are equal, so the lines are coincident.
By using this method, we can analyze the relationship between two lines based on the coefficients and constants of their linear equations without needing to solve a system of linear equations.
And so on.
