Distance Between Two Lines
The distance between two lines is defined as the minimum distance between points on the lines. $$ d(r_1, r_2) := min(P_{r1}, P_{r2}) $$
To measure the distance between two parallel lines, take a point P(x0; y0) on one line and measure the distance from point P to the other line $ ax+by+c=0 $
$$ d = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$
Alternatively, if you know the slope m of two parallel lines $ y=mx+q_1 $ and $ y=mx+q_2 $
$$ d = \frac{|q_2-q_1|}{\sqrt{1+m^2}} $$
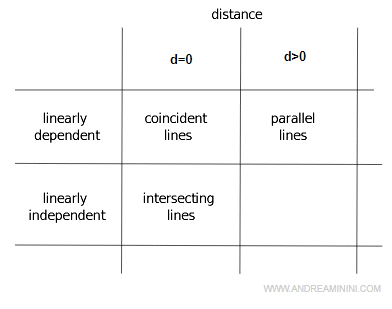
There are the following cases:
- Zero Distance. If the minimum distance is zero, the two lines are either coincident (if linearly dependent) or intersecting (if linearly independent).
- Finite Distance. If the minimum distance is a positive finite number, the two lines are parallel.
This diagram summarizes the different possibilities.
How to Calculate the Distance Between Lines
First, determine if the lines are parallel, coincident, or intersecting by examining the linear dependence of the direction vectors.
1] Linearly Dependent Lines
If the direction vectors are linearly dependent, the lines are either coincident or parallel.
How to determine if they are coincident or parallel?
Take a point from one of the lines and calculate the distance to the other line.
- Parallel ( d>0 ). If the distance is greater than zero, the lines are parallel.
- Coincident ( d=0 ). If the distance is zero, the lines are coincident.
2] Linearly Independent Lines
If the direction vectors are linearly independent, the lines will always intersect.
Therefore, there is only one common point (point of intersection) between the two lines.
The minimum distance is zero.
Practical Examples
Example 1
We have two lines:
$$ r_1: 5x+3y-6=0 $$
$$ r_2: -4x+4y-8=0 $$
First, check if they are linearly independent.
Take the respective normal vectors:
$$ n_1 = \begin{pmatrix} 5 \\ 3 \end{pmatrix} $$
$$ n_2 = \begin{pmatrix} -4 \\ 4 \end{pmatrix} $$
Note. Linear dependence can be verified using either the normal vectors or the direction vectors. Since they are orthogonal vectors, if the normal vectors are linearly independent, so are the direction vectors, and vice versa.
Next, calculate the determinant of the matrix formed by the vectors to see if they are linearly independent.
$$ det \begin{pmatrix} 5 & -4 \\ 3 & 4 \end{pmatrix} = 20 + 12 = 32 $$
The determinant is not zero.
This means the two vectors are linearly independent.
Therefore, the two lines intersect, and the minimum distance is zero.
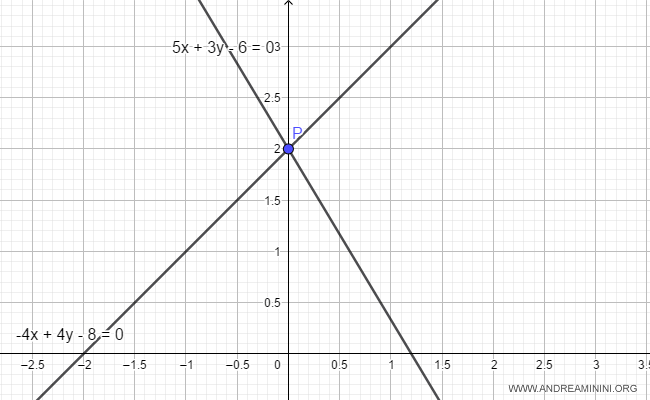
Note. To find the point of intersection, solve the system of equations formed by both lines: $$ \begin{cases} 5x+3y-6=0 \\ -4x+4y-8=0 \end{cases} $$ $$ \begin{cases} x=\frac{6-3y}{5} \\ -4(\frac{6-3y}{5})+4y-8=0 \end{cases} $$ $$ \begin{cases} x=\frac{6-3y}{5} \\ y=2 \end{cases} $$ $$ \begin{cases} x=\frac{6-3(2)}{5} \\ y=2 \end{cases} $$ $$ \begin{cases} x=0 \\ y=2 \end{cases} $$
Example 2
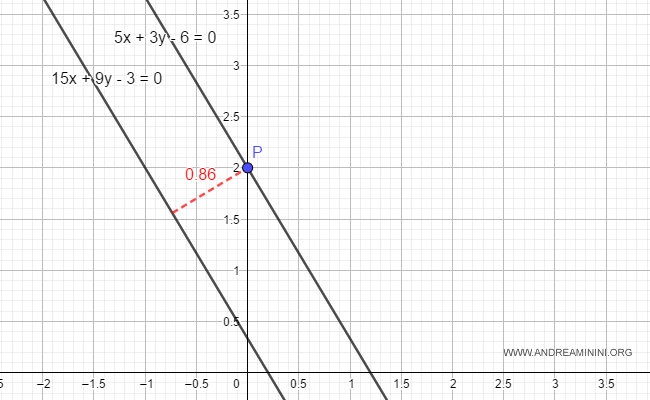
We have two lines:
$$ r_1: 5x+3y-6=0 $$
$$ r_2: 15x+9y-3=0 $$
First, check if they are linearly independent.
Take the respective normal vectors:
$$ n_1 = \begin{pmatrix} 5 \\ 3 \end{pmatrix} $$
$$ n_2 = \begin{pmatrix} 15 \\ 9 \end{pmatrix} $$
Next, calculate the determinant of the matrix formed by the vectors to see if they are linearly independent.
$$ det \begin{pmatrix} 5 & 15 \\ 3 & 9 \end{pmatrix} = 45 - 45 = 0 $$
The determinant is zero.
This means the two vectors are linearly dependent.
Therefore, the two lines can be either parallel or coincident.
How to determine if they are parallel or coincident?
Take any point from line r1.
For example:
$$ P = \begin{pmatrix} 0 \\ 2 \end{pmatrix} $$
Then calculate the distance between point P and the other line r2.
$$ D(P(x_0,y_0),r_2) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$
$$ D(P(0,2),r_2) = \frac{|15x+9y-3|}{\sqrt{15^2+9^2}} $$
$$ D(P(0,2),r_2) = \frac{|15(0)+9(2)-3|}{\sqrt{225+81}} $$
$$ D(P(0,2),r_2) = \frac{|15|}{\sqrt{306}} = 0.86 $$
The distance between point P and line r2 is greater than zero.
Therefore, the two lines are parallel.
Note. If the distance had been zero, the two lines would have been coincident.
