How to Represent a Line Using a Vector

A geometric vector defines a direction that is shared by all lines in the plane parallel to it.

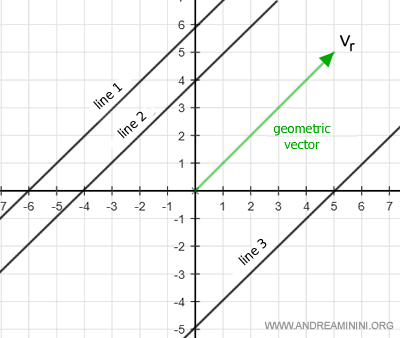
Therefore, any line in the plane can be described by:

• a non-trivial geometric vector v_r, known as the direction vector, indicating the direction of the line: $$ v_r = \begin{pmatrix} l \\ m \end{pmatrix} $$

  The parameters l and m are the direction parameters of the line.

• a specific point P₀ on the plane through which the line passes: $$ P_0 = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} $$

  Example
  

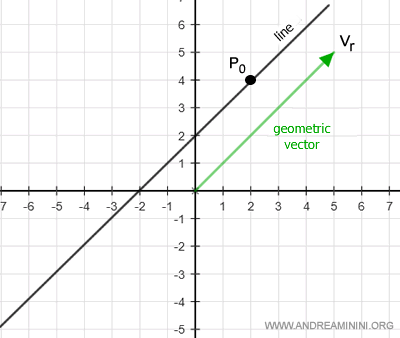
A point on the plane belongs to the line if there exists a scalar α such that

$$ OP = OP_0 + α v_r $$

Example

Consider the point P₁ with coordinates (-5, -3).

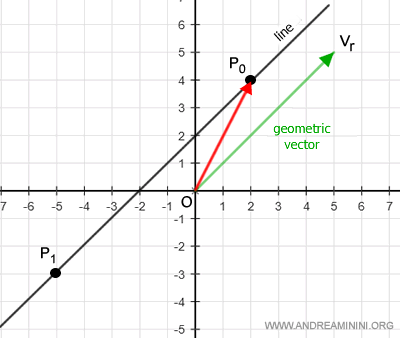
The point P₁ belongs to the line if

$$ OP_1 = OP_0 + α v_r $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + α \begin{pmatrix} 5 \\ 5 \end{pmatrix} $$

Solving the system of equations to find the scalar α:

$$ \begin{cases} -5 = 2 + α5 \\ -3 = 4 + α5 \end{cases} = \begin{cases} α = - \frac{7}{5} \\ α = - \frac{7}{5} \end{cases} $$

The system solves with the scalar α = -7/5.

In fact:

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + α \begin{pmatrix} 5 \\ 5 \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} 5α \\ 5α \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} 5 \cdot ( - \frac{7}{5} ) \\ 5 \cdot ( - \frac{7}{5} ) \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} -7 \\ -7 \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 - 7 \\ 4 - 7 \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} -5 \\ -3 \end{pmatrix} $$

We can generalize this result by stating that

All coordinates of all points on the line are characterized by the following equation, called the vector equation of the line: $$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + α \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$Converting the vector equation into a system of equations, we get the parametric equations of the line:$$ \begin{cases} x = x_0 + α l \\ y = y_0 + α m \end{cases} $$

There are infinitely many vector and parametric equations because there are infinitely many multiples of the direction vector.

Cartesian Equations

The vector P₀P₁ is parallel to the direction vector v_r.

According to theory, a vector is parallel and proportional to another if

$$ \begin{pmatrix} x-x_0 & l \\ y - y_0 & m \end{pmatrix} \le 1 $$

This is true if

$$ det \begin{pmatrix} x-x_0 & l \\ y - y_0 & m \end{pmatrix} = 0 $$

Calculating the determinant, we get

$$ m ( x-x_0 ) - l ( y - y_0 ) = 0 $$

This gives us the Cartesian equation.

Similarly, there are infinitely many Cartesian equations.