Equation of a Line Passing Through Two Points

The equation of a line passing through two distinct points \( (x_1, y_1) \) and \( (x_2, y_2) \) in the plane can be determined using the following formula: $$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$ Exactly one unique line passes through any two distinct points in the plane.

For two distinct points in space, \( (x_1, y_1, z_1) \) and \( (x_2, y_2, z_2) \), the equation of the line passing through them is given by: $$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} = \frac{z - z_1}{z_2 - z_1} $$ which can also be expressed as: $$ \begin{cases} \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \\ \\ \frac{y - y_1}{y_2 - y_1} = \frac{z - z_1}{z_2 - z_1} \end{cases} $$ provided that the two points are distinct, i.e. $ x_1 \ne x_2 $, $ y_1 \ne y_2 $, and $ z_1 \ne z_2 $.

This representation is known as the fractional form of the line equation.

It can be used to derive the equation of the line in the form:

$$ ax + by + c = 0 $$

It’s also referred to as the collinearity condition, as it allows you to verify whether three points \( (x, y) \), \( (x_1, y_1) \), and \( (x_2, y_2) \) lie on the same straight line.

• If the point $ (x, y) $ satisfies this proportion, then it lies on the line determined by $ (x_1, y_1) $ and $ (x_2, y_2) $.
• If it does not satisfy the proportion, the point is not collinear with the other two.

Example

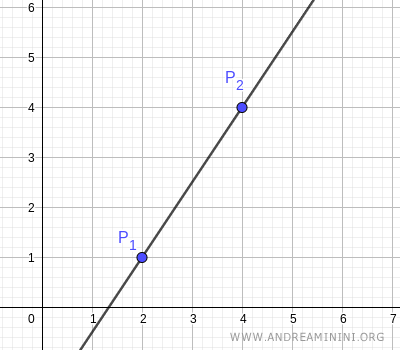
I need to find the equation of the line passing through two distinct points A and B on the plane.

Point A is located at coordinates \( (x_1,y_1)=(1, 2) \) and point B at coordinates \( (x_2,y_2)= (4, 5) \)

I use the formula for the line passing through two points.

$$ \frac{y-y_1}{y_2-y_1}= \frac{x-x_1}{x_2-x_1} $$

In this case, the coordinates of the two points are \( x_1=1 \), \( y_1=2 \) and \( x_2=4 \), \( y_2=5 \).

$$ \frac{y-2}{5-2}= \frac{x-1}{4-1} $$

$$ \frac{y-2}{3}= \frac{x-1}{3} $$

By multiplying both sides by 3, we simplify the equation.

$$ \frac{y-2}{3} \cdot 3= \frac{x-1}{3} \cdot 3 $$

$$ y-2 = x-1 $$

Move all terms to one side of the equation.

$$ y - 2 - x + 1= 0 $$

$$ y - x -1 = 0 $$

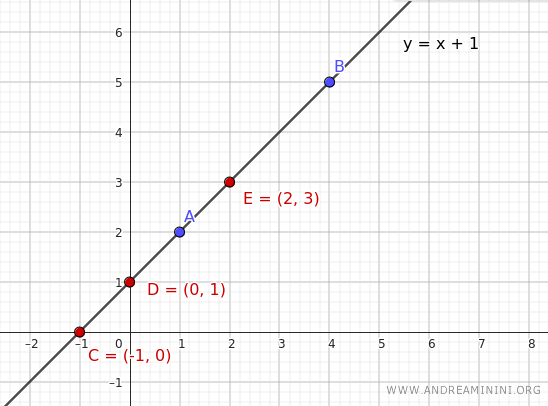
Thus, we find the implicit form of the equation y-x-1=0 for the line passing through the points (1,2) and (4,5).

To convert to explicit form, solve for y in terms of the other variables.

$$ y = x+1 $$

Next, substitute different values for the independent variable x to find the corresponding y values.

$$ \begin{array}{c|c} x & y=x+1 \\ \hline -1 & 0 \\ 0 & 1 \\ 1 & 2\\ 2 & 3 \end{array} $$

This gives us additional points on the line.

 

Alternative Solution

Alternatively, you can use the coordinates of the two points to calculate the slope (m) of the line, which is given by:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

This formula indicates how much the line "rises" or "falls" as you move from left to right along the x-axis.

Given the coordinates \( x_1=1 \), \( y_1=2 \), and \( x_2=4 \), \( y_2=5 \).

$$ m = \frac{5 - 2}{4 - 1} $$

$$ m = \frac{3}{3} $$

$$ m = 1 $$

Once you have the slope, you can use the point-slope form of the line equation:

$$ y - y_1 = m \cdot (x - x_1) $$

Substituting \( m=1 \).

$$ y - y_1 = 1 \cdot (x - x_1) $$

$$ y - y_1 = x - x_1 $$

Given \( x_1=1 \), \( y_1=2 \)

$$ y - 2 = x - 1 $$

Solve for y to get the line equation

$$ y = x - 1 + 2 $$

$$ y = x + 1 $$

The final result is always the same.

The equation of the line passing through the points \( (1, 2) \) and \( (3, 8) \) is \( y = 3x - 1 \).

Example 2

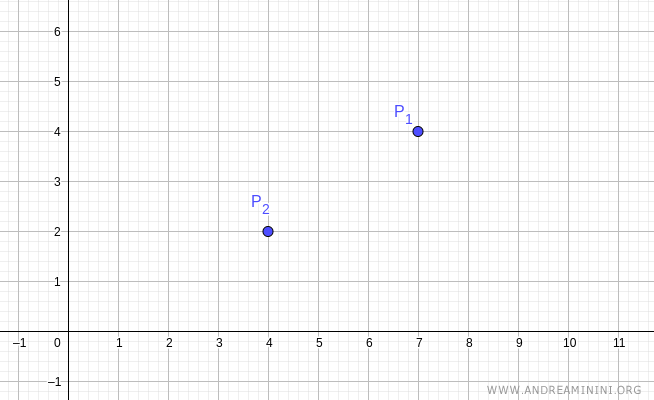
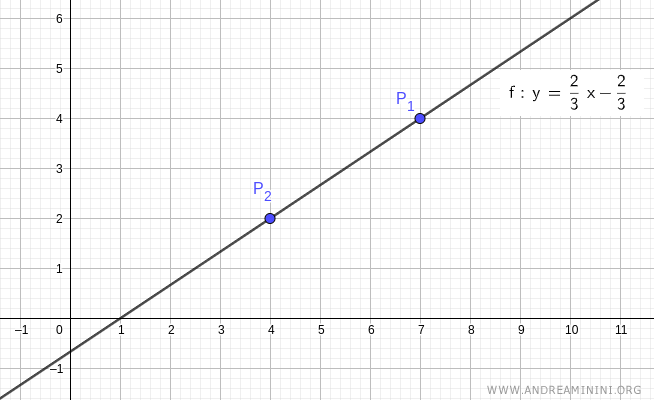
Let’s consider two distinct points on the plane: P₁(7,4) and P₂(4,2).

The equation of the line passing through points P₁ and P₂ is:

$$ \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1} $$

Here, (x₁, y₁) = (7,4) and (x₂, y₂) = (4,2).

Substituting the values x₁=7, x₂=4, y₁=4, and y₂=2, we get:

$$ \frac{x-7}{4-7} = \frac{y-4}{2-4} $$

$$ \frac{x-7}{-3} = \frac{y-4}{-2} $$

Now, let’s solve for y:

$$ \frac{x}{-3} + \frac{-7}{-3} = \frac{y}{-2} + \frac{-4}{-2} $$

$$ \frac{y}{-2} = \frac{x}{-3} + \frac{-7}{-3} - 2 $$

$$ y = (-2) \cdot \left[ \frac{x}{-3} + \frac{7-6}{3} \right] $$

$$ y = (-2) \cdot \left[ \frac{x}{-3} + \frac{1}{3} \right] $$

$$ y = \frac{2}{3}x - \frac{2}{3} $$

This is the explicit equation of the line passing through the points P₁(7,4) and P₂(4,2).

By varying x, you can find all the points on this line.

Example 3

Let’s consider three points in the plane:

$$ A(1,2), \quad B(3,6), \quad C(5,10). $$

We want to determine whether the points $A$, $B$, and $C$ are collinear.

To check this, we can use the fractional form of the line equation.

First, let’s consider points $A$ and $B$:

$$ x_1 = 1, \; y_1 = 2, \quad x_2 = 3, \; y_2 = 6. $$

The condition for point $C(x,y) = (5,10)$ to lie on the same line as $A$ and $B$ is:

$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$

Substituting the coordinates, we get:

$$ \frac{10 - 2}{6 - 2} = \frac{5 - 1}{3 - 1} $$

$$ \frac{8}{4} = \frac{4}{2} \quad \Rightarrow \quad 2 = 2 $$

Since the equality holds, the three points are collinear. In other words, there is a single straight line passing through all three points.

What is the equation of this line? Let’s use points $$ A(1,2) $$ and $$ B(3,6) $$ to find it. First, we calculate the slope $m$: $$ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2 $$ We then write the equation in slope-intercept form, starting from the point-slope equation with point $A(1,2)$: $$ y - y_1 = m(x - x_1) $$ Substituting the values: $$ y - 2 = 2(x - 1) $$ Simplifying: $$ y = 2(x - 1) + 2 $$ $$ y = 2x - 2 + 2 $$ $$ y = 2x $$ Thus, the slope-intercept form of the line passing through all three points is $ y = 2x $. To express it in standard form, $ ax + by + c = 0 $, we rearrange: $$ y - 2x = 0 $$ Optionally, we can multiply both sides by $ -1 $ to keep the $ x $ coefficient positive: $$ 2x - y = 0 $$ Therefore, the standard (implicit) form of the line is: $$ 2x - y = 0 $$

Alternative Solution

Another approach to verify collinearity is by comparing slopes.

First, compute the slope $ m_{AB} $:

$$ m_{AB} = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2 $$

Then compute the slope $ m_{BC} $:

$$ m_{BC} = \frac{10 - 6}{5 - 3} = \frac{4}{2} = 2 $$

Since $ m_{AB} = m_{BC} $, the three points lie on the same straight line.

Method 3 (Using the Area of the Triangle). A further method involves calculating the area of triangle $ABC$: $$ \text{Area} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| $$ Substituting the coordinates: $$ \begin{align} \text{Area} &= \frac{1}{2} \left| 1(6 - 10) + 3(10 - 2) + 5(2 - 6) \right| \\ &= \frac{1}{2} \left| -4 + 24 - 20 \right| \\ &= \frac{1}{2} \times 0 = 0 \end{align} $$ Since the area is zero, the points are collinear.

Example 4

Let’s now consider two points in three-dimensional space, $ \mathbb{R}^3 $:

$$ P_1(1,2,3), \quad P_2(5,6,7) $$

We want to determine the equation of the line passing through $P_1$ and $P_2$.

We set up the following system of equations:

$$ \begin{cases} \dfrac{y - y_1}{y_2 - y_1} = \dfrac{x - x_1}{x_2 - x_1} \\ \\ \dfrac{y - y_1}{y_2 - y_1} = \dfrac{z - z_1}{z_2 - z_1} \end{cases} $$

Substituting the coordinates of $ P_1(1,2,3) $ and $ P_2(5,6,7) $ gives:

$$ \begin{cases} \dfrac{y - 2}{6 - 2} = \dfrac{x - 1}{5 - 1} \\ \\ \dfrac{y - 2}{6 - 2} = \dfrac{z - 3}{7 - 3} \end{cases} $$

$$ \begin{cases} \dfrac{y - 2}{4} = \dfrac{x - 1}{4} \\ \\ \dfrac{y - 2}{4} = \dfrac{z - 3}{4} \end{cases} $$

We simplify by multiplying both sides of each equation by 4:

$$ \begin{cases} y - 2 = x - 1 \\ \\ y - 2 = z - 3 \end{cases} $$

Solving for $ x $ and $ y $, we have:

$$ \begin{cases} x = y - 1 \\ \\ y = z - 1 \end{cases} $$

Thus, the line is represented by the reduced system:

$$ \begin{cases} x = y - 1 \\ \\ y = z - 1 \end{cases} $$

Below is a graphical representation of the line passing through points $ P_1 $ and $ P_2 $ in three-dimensional space.

Note. To check whether a point, such as $ Q(9,10,11) $, lies on the line, we substitute its coordinates into the system and verify whether the equations are satisfied: $$ \begin{cases} x = y - 1 \\ \\ y = z - 1 \end{cases} $$ $$ \begin{cases} 9 = 10 - 1 \\ \\ 10 = 11 - 1 \end{cases} $$ $$ \begin{cases} 9 = 9 \\ \\ 10 = 10 \end{cases} $$ Since both equations hold true, point $ Q $ lies on the line.

Proof

To prove the formula for the line passing through two points, consider three points on the plane \( (x_1;y_1) \), \( (x_2;y_2) \), \( (x;y) \).

Assume that the same line passes through each point.

Thus, we construct a system of equations.

$$ \begin{cases} ax_1+by_1+c=0 \\ ax_2+by_2+c=0 \\ ax+by+c=0 \end{cases} $$

Using the reduction method, subtract the first equation from the second and third equations.

$$ \begin{cases} a(x_2-x_1)+b(y_2-y_1)=0 \\ a(x-x_1)+b(y-y_1)=0 \end{cases} $$

$$ \begin{cases} a(x_2-x_1) = - b(y_2-y_1) \\ a(x-x_1) = - b(y-y_1) \end{cases} $$

$$ \begin{cases} \frac{x_2-x_1}{y_2-y_1}= - \frac{b}{a} \\ \frac{x-x_1}{y-y_1}= - \frac{b}{a} \end{cases} $$

By comparing the two equations, it is evident that both are equal to -b/a.

Therefore, we can write the equality as follows:

$$ \frac{x_2-x_1}{y_2-y_1}= \frac{x-x_1}{y-y_1} $$

Finally, with a simple algebraic step, we obtain the collinearity condition

$$ \frac{y-y_1}{y_2-y_1}= \frac{x-x_1}{x_2-x_1} $$

This proves the formula for the equation of a line passing through two distinct points \( (x_1;y_1) \) and \( (x_2;y_2) \) on the plane.

Alternative Approach

Let's consider two distinct points in the plane: P₁(x₁, y₁) and P₂(x₂, y₂).

We'll use the concept of a line bundle to derive the equation of lines that pass through point P₁.

$$ y - y_1 = m(x - x_1) $$

Here, m is the slope of the line, which can take on infinitely many values - one for each possible inclination of the line, except for the line parallel to the y-axis.

The slope of the line passing through the points P₁ and P₂ is given by:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

Substituting this slope into the equation of the line bundle passing through point P₁, we have:

$$ y - y_1 = m(x - x_1) $$

$$ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1) $$

Now, let's separate the variables y and x on both sides of the equation:

$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$

This gives us the equation of the line passing through the two points.

Line Passing Through Two Points in Linear Algebra

We can also demonstrate the equation of the line passing through two points using the framework of linear algebra.

This approach requires some familiarity with vector and matrix operations.

Proof

Given two points in the plane:

$$ P_1 \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} $$ $$ P_2 \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} $$

The line passing through P₁ and P₂ can be represented by the following direction vector P₁P₂:

$$ v_r \equiv \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \end{pmatrix} $$

Using this direction vector, we can write the vector equation of the line as:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} + t \cdot \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \end{pmatrix} $$

From this, we can derive the system of parametric equations for the line, starting from P₁:

$$ \begin{cases} x = x_1 + t \cdot (x_2 - x_1) \\ y = y_1 + t \cdot (y_2 - y_1) \end{cases} $$

Note: Starting from P₂ would yield a different set of parametric equations, but the final result remains the same. Therefore, for this demonstration, we can choose either set of parametric equations. $$ \begin{cases} x = x_2 + t \cdot (x_2 - x_1) \\ y = y_2 + t \cdot (y_2 - y_1) \end{cases} $$

For a generic point P on the line, this forms a vector relative to point P₁:

$$ \overrightarrow{P_1P} = P - P_1 = \begin{pmatrix} x - x_1 \\ y - y_1 \end{pmatrix} $$

This vector P₁P must be parallel and proportional to the direction vector P₁P₂ because it lies on the same line r, which is defined by the direction vector v_r.

Therefore, the two vectors P₁P and P₁P₂ must be linearly dependent.

Placing the two vectors as columns in a matrix, the determinant must be zero.

$$ det \begin{pmatrix} x - x_1 & x_2 - x_1 \\ y - y_1 & y_2 - y_1 \end{pmatrix} = 0 $$

Calculating the determinant, we get:

$$ (x - x_1) \cdot (y_2 - y_1) - (x_2 - x_1) \cdot (y - y_1) = 0 $$

With a few more algebraic steps, this leads to the Cartesian equation of the line:

$$ (x - x_1) \cdot (y_2 - y_1) = (x_2 - x_1) \cdot (y - y_1) $$

$$ \frac{x - x_1}{x_2 - x_1} = \frac{y - y_1}{y_2 - y_1} $$

This gives us the general formula for the equation of the line passing through two points.

And that concludes the demonstration.

A Practical Example

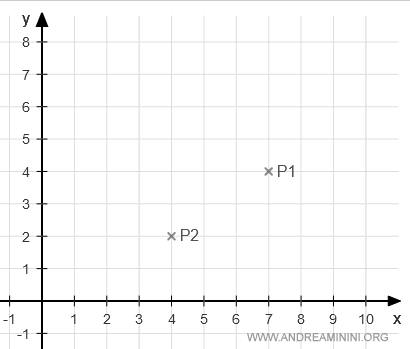
Let's consider two points in the plane: P₁ and P₂.

$$ P_1 \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = P_1 \begin{pmatrix} 7 \\ 4 \end{pmatrix} $$

$$ P_2 \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = P_2 \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$

Their graphical representation is as follows:

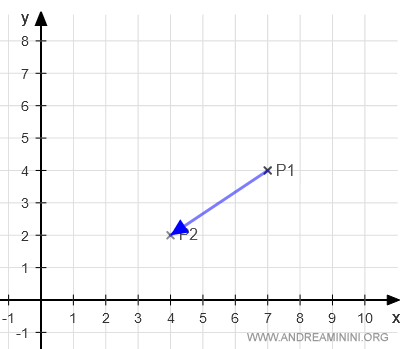
If we fix a direction from P₁ to P₂, we obtain the vector P₁P₂:

$$ \overrightarrow{P_1P_2} = P_2 - P_1 = \begin{pmatrix} 4 \\ 2 \end{pmatrix} - \begin{pmatrix} 7 \\ 4 \end{pmatrix} = \begin{pmatrix} 4 - 7 \\ 2 - 4 \end{pmatrix} = \begin{pmatrix} -3 \\ -2 \end{pmatrix} $$

The vector equation of the line is:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} + t \cdot \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 7 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 4 - 7 \\ 2 - 4 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 7 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} -3 \\ -2 \end{pmatrix} $$

From this, we can derive the parametric equation of the line:

$$ \begin{cases} x = 7 - 3t \\ y = 4 - 2t \end{cases} $$

Using the parametric equation, we can plot all the points on the line by varying the value of the parameter t.

Therefore, a generic point on the line can be expressed as:

$$ P \begin{pmatrix} 7 - 3t \\ 4 - 2t \end{pmatrix} \quad \text{where} \quad t \in \mathbb{R} $$

When t = 0, we get the point P₁, which is the starting point of the vector P₁P₂.

As t increases, the point moves toward P₂.

When t = 1, we reach P₂, the endpoint of the vector P₁P₂.

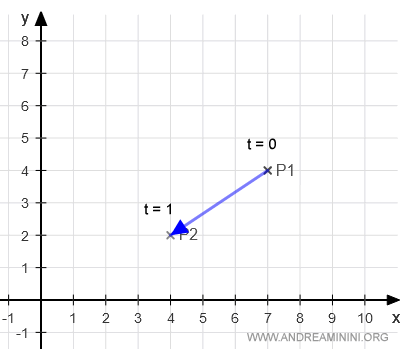
Now let's find the Cartesian equations.

A line r also passes through points P₁ and P₂.

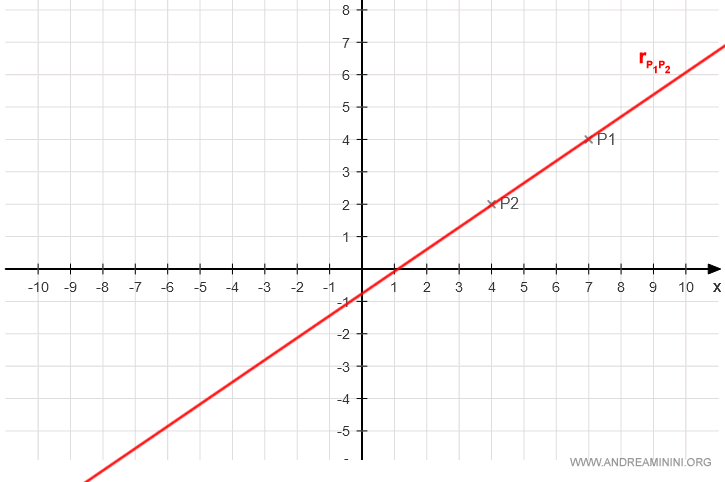
For a generic point P on line r:

$$ P \begin{pmatrix} x \\ y \end{pmatrix} $$

The point P and the starting point P₁ form another vector, P₁P:

$$ \overrightarrow{P_1P} = \begin{pmatrix} x \\ y \end{pmatrix} - \begin{pmatrix} 7 \\ 4 \end{pmatrix} $$

$$ \overrightarrow{P_1P} = \begin{pmatrix} x - 7 \\ y - 4 \end{pmatrix} $$

The vector P₁P, which lies on line r, is proportional to the geometric vector P₂P₁ we calculated earlier (i.e., v_r), because line r passes through the same points P₁ and P₂.

$$ \overrightarrow{P_1P} = \begin{pmatrix} x - 7 \\ y - 4 \end{pmatrix} $$

$$ \overrightarrow{P_1P_2} = \begin{pmatrix} -3 \\ -2 \end{pmatrix} $$

The two vectors are proportional vectors if they are linearly dependent.

In this case, the determinant of the matrix formed by the two vectors as columns must be zero.

$$ det \begin{pmatrix} x - 7 & -3 \\ y - 4 & -2 \end{pmatrix} = 0 $$

Calculating the determinant gives us the Cartesian equation of the line:

$$ (x - 7)(-2) - (-3)(y - 4) = 0 $$

$$ -2x + 14 + 3y - 12 = 0 $$

$$ -2x + 3y + 2 = 0 $$

We can now express one of the coordinates, x or y, in terms of the other.

$$ y = \frac{2x - 2}{3} $$

Why is knowing the Cartesian equation useful? It allows us to determine whether a point in the plane with coordinates (x, y) lies on the line.

And so on.