Polar Equation of a Line
- The equation of a line in polar form:
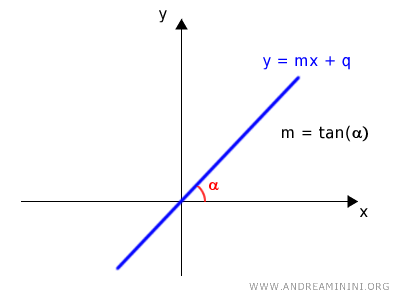
- If the line passes through the origin, it's enough to know the angle α, which determines the slope (m) of the line y = mx + q, where $$ m = \tan \alpha \ \ \ \ with \ \alpha \ne \frac{\pi}{2}+k \pi $$ and q = 0.
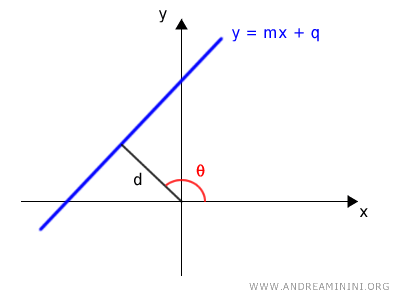
- If the line doesn't pass through the origin, you'll need to know the distance d between the line and the pole (origin), as well as the angle β of the distance segment relative to the positive polar axis $$ d = r \cdot \cos ( \beta - \alpha) $$
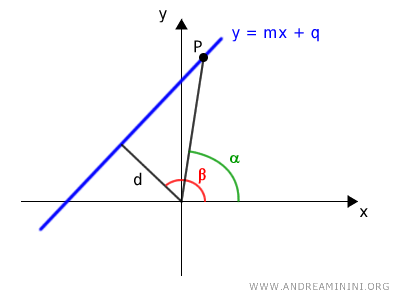
Here, α represents the angle in the polar coordinates of another point P on the line.
The difference θ=β-α is the interior angle between the two segments.
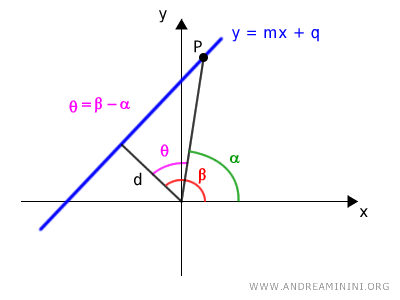
Obviously, if the line passes through the origin, the distance d=0 is zero.
A Practical Example
Example 1: Converting from Cartesian to Polar Form
Consider the line
$$ y = 2x + 3 $$
We need to find the polar coordinates of this line.
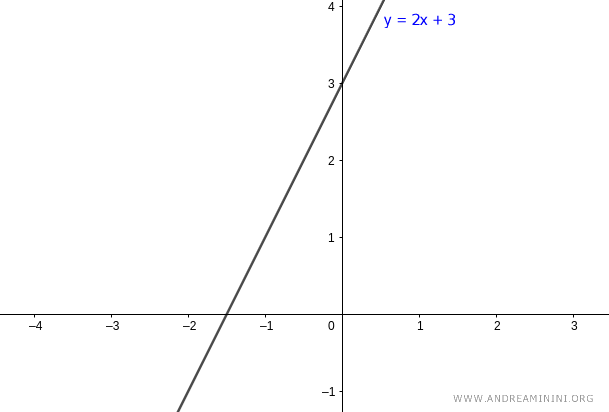
The slope of the line is m=2
$$ m = 2 $$
Thus, the angle between the line and the polar axis is
$$ m = \tan \alpha $$
Taking the arctangent of both sides, we have
$$ \arctan(m) = \arctan(\tan \alpha) $$
$$ \arctan(m) = \alpha $$
Given that m = 2
$$ \alpha = \arctan(2) $$
$$ \alpha = 63.43° $$
So, the angle between the line and the polar axis is α = 63.43°
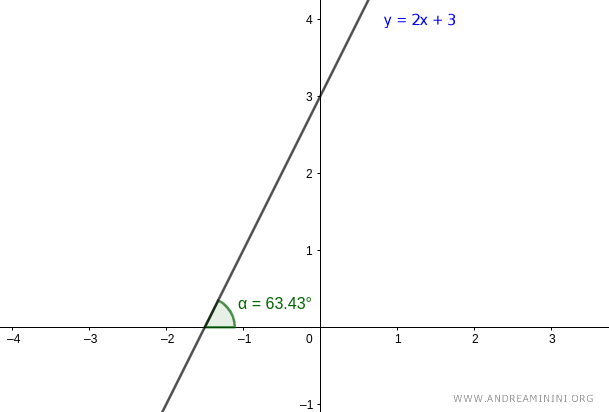
We've now determined one of the parameters of the line's polar coordinates.
Next, we need to calculate the other parameter, the distance (d) between the line and the pole (origin).
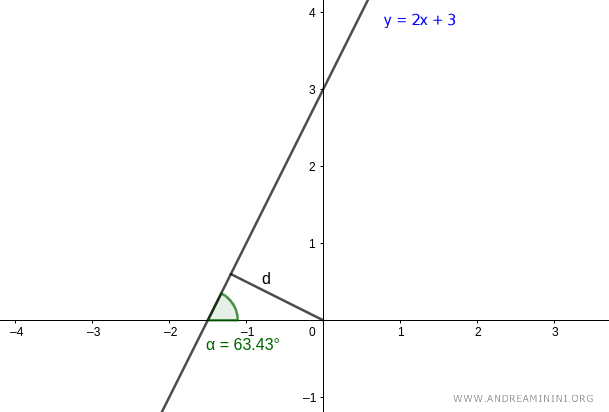
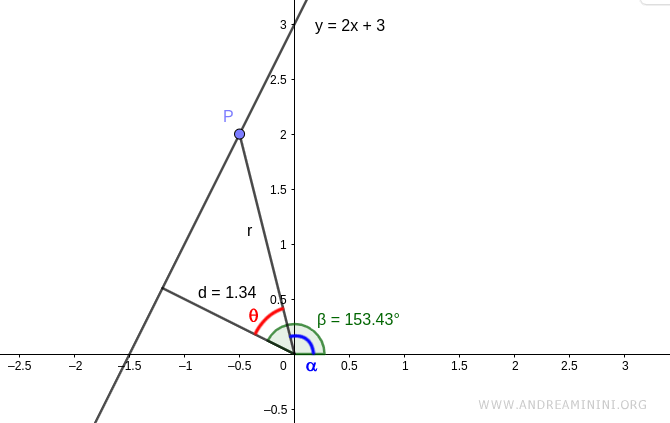
Let's take another point P on the line.
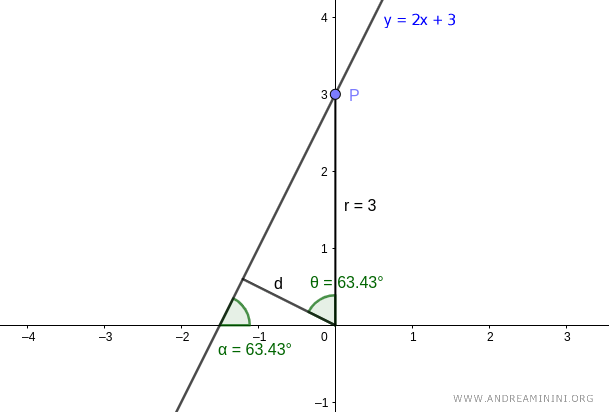
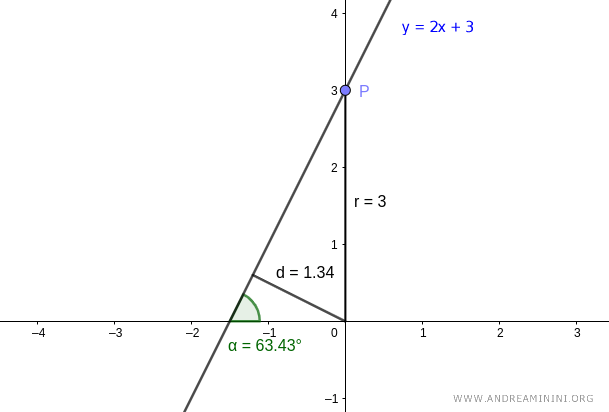
For simplicity, let's use point P at coordinates (0,3) with r=3. This way, the angle θ between the two segments coincides with the angle α, so θ = α = 63.43°
Note. Any other point P on the line would work just as well.
Now that we know the angle θ=63.43° and the length r=3, we can calculate the distance (d)
$$ d = r \cdot \cos ( θ ) $$
$$ d = 3 \cdot \cos ( 63.43° ) $$
$$ d = 1.34 $$
So, we've found the minimum distance (d) between the line and the pole.
The polar coordinates of the line are therefore [63.43°, 1.34]
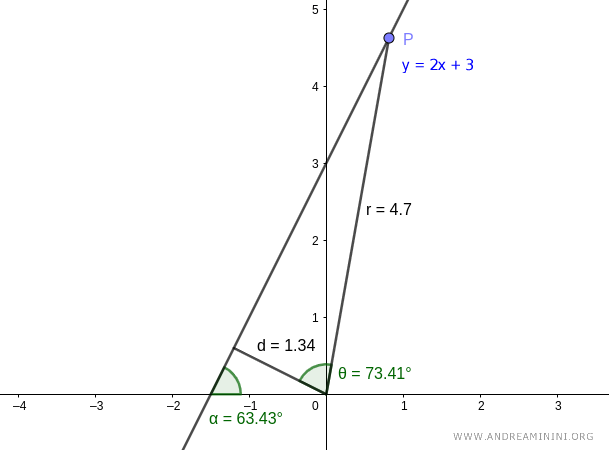
Note. As mentioned earlier, any other point P on the line would have yielded the same result. For example, choosing a different point P with different coordinates would give a different internal angle θ=73.41° and a length r=4.7, but still result in the same distance d=4.7·cos(73.41°)=1.34.
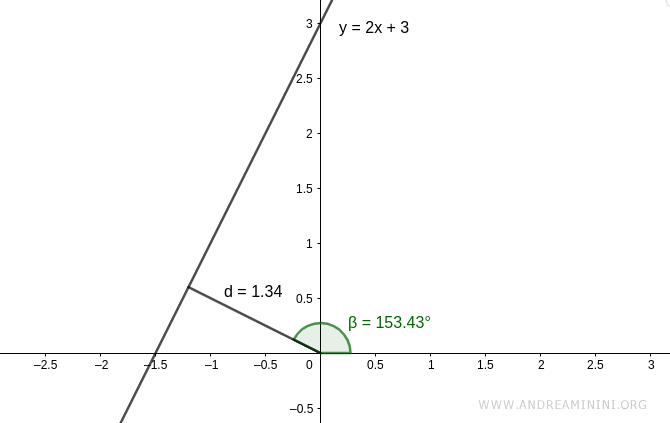
Example 2: Converting from Polar to Cartesian Form
Now, consider a line given in polar form
$$ d = 1.34 $$
$$ \beta = 153.43 $$
We need to derive the Cartesian equation y=mx+q from this information.
Consider the polar coordinates [α,r] of a generic point P on the line.
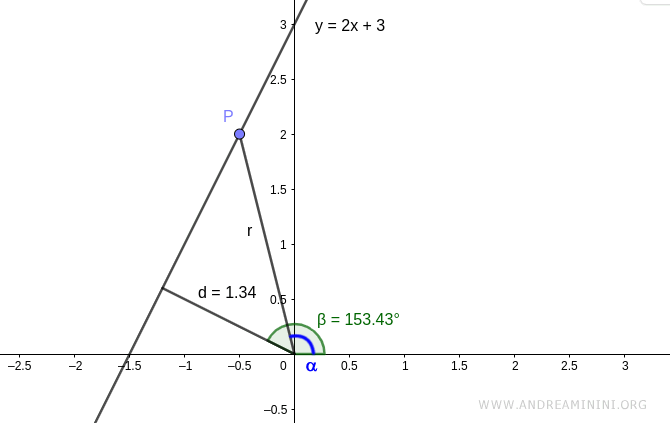
We know the distance (d) of the line from the pole (origin) is given by the formula
$$ d = r \cdot \cos (θ) $$
Where θ is the internal angle between the two segments d and r, which can also be found as the difference between the angles θ=β-α
Knowing θ=β-α, we can rewrite the distance formula as
$$ d = r \cdot \cos (\beta - \alpha) $$
We know the angle β=153.43°
$$ d = r \cdot \cos (153.43° - \alpha) $$
And we know the distance d=1.34
$$ 1.34 = r \cdot \cos (153.43° - \alpha) $$
Using the cosine subtraction formula, which states that cos(β-α)=cos(β)cos(α)+sin(β)sin(α), we get
$$ 1.34 = r \cdot [ \cos (153.43°) \cos (\alpha) + \sin(153.43°) \sin(\alpha) ] $$
$$ 1.34 = r \cdot \cos (153.43°) \cos (\alpha) + r \cdot \sin(153.43°) \sin(\alpha) $$
Knowing that x=r·cos(α)
$$ 1.34 = [ r \cdot \cos (\alpha) ] \cos (153.43°) + r \cdot \sin(153.43°) \sin(\alpha) $$
$$ 1.34 = x \cdot \cos (153.43°) + r \cdot \sin(153.43°) \sin(\alpha) $$
And that y=r ·sin(α)
$$ 1.34 = x \cdot \cos (153.43°) + [ r \cdot \sin(\alpha) ] \sin(153.43°) $$
$$ 1.34 = x \cdot \cos (153.43°) + y \cdot \sin(153.43°) $$
We can now solve for y
$$ y = \frac{ 1.34 } { \sin(153.43°) } - x \cdot \frac{ \cos (153.43°) }{ \sin(153.43°) } $$
The ratio cos(153.43°)/sin(153.43°) equals -2
$$ y = \frac{ 1.34 } { \sin(153.43°) } - x \cdot (-2) $$
$$ y = \frac{ 1.34 } { \sin(153.43°) } + 2x $$
The ratio 1.34/sin(153.43°) equals 3
$$ y = 3 + 2x $$
This gives us the Cartesian equation of the line.
The Proof
1) The Line Passing Through the Origin
For a line passing through the origin, q=0
$$ y = m \cdot x $$
Graphically:
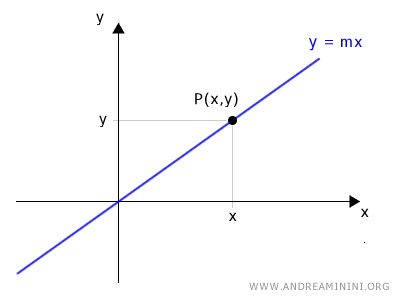
Let’s take any point P on the line.
This point P has Cartesian coordinates (x,y).
We draw a segment between the origin O and point P.
The segment OP has a length r and an angle α relative to the x-axis.
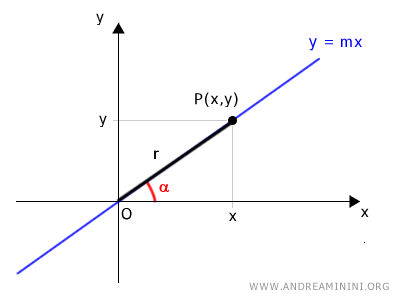
Knowing the angle α and the length of the segment OP, the Cartesian coordinates (x,y) of point P can be expressed using the sine and cosine functions.
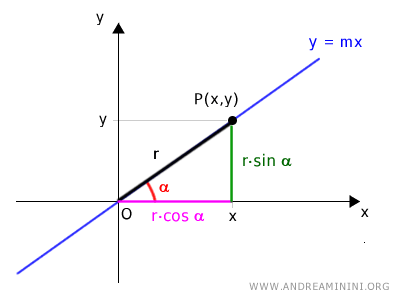
So, the polar coordinates of point P are [r,α]
$$ y = r \cdot \sin \alpha $$ $$ x = r \cdot \cos \alpha $$
Substituting x and y in trigonometric form into the equation of the line:
$$ y = m \cdot x $$
$$ r \cdot \sin \alpha = m \cdot (r \cdot \cos \alpha) $$
Simplifying by canceling out r from both sides:
$$ \sin \alpha = m \cdot \cos \alpha $$
We can now find the slope m of the line:
$$ m = \frac{\sin \alpha}{\cos \alpha} $$
According to the second principle of trigonometry, tan α = sin α/cos α
So, we replace the sine-to-cosine ratio with the tangent.
$$ m = \tan \alpha $$
The tangent is undefined at 90° (π/2) and its multiples 90°±k·180° or π/2±k·π
$$ m = \tan \alpha \ \ \ \ with \ \alpha \ne \frac{\pi}{2}+k \pi $$
Where k is any integer.
This completes the proof of the polar equation for a line passing through the origin.
2) The Equation of a Line Not Passing Through the Origin
Now, let’s consider a line that passes through a point P on the plane but not through the origin.
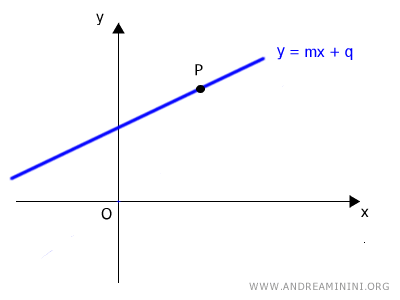
Any line that doesn’t pass through the origin can be uniquely identified by two polar parameters:
- the distance (d) between the line and the pole
- the angle β between the line of distance and the polar axis
The distance (minimum) between the line and the pole is the segment OA, which passes through the origin (pole) and is perpendicular to the line.
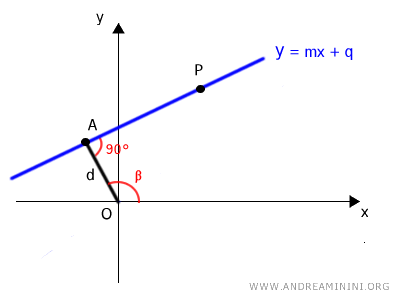
The segment OA forms an angle β with the polar axis and has a length d, which we need to calculate.
To determine this distance (d), we draw a segment OP between the pole and point P on the line.
The segment OP forms an angle α with the polar axis.
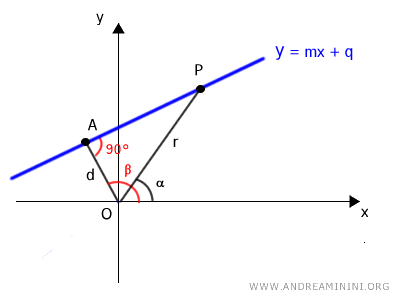
This forms a right triangle OAP.
This allows us to use the theorems of right triangles.
According to the first theorem of right triangles, the length of one leg (OA) is equal to the product of the hypotenuse (OP) and the cosine of the acute angle θ=AOP:
$$ \overline{OA} = \overline{OP} \cdot \cos \widehat{AOP} $$
Where the angle θ=AOP is the acute angle adjacent to leg OA.
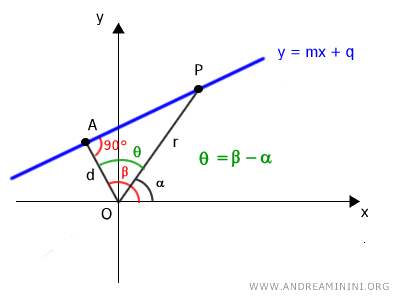
The angle θ=OAP can also be written as the difference between angles beta and alpha: θ=β-α
$$ \overline{OA} = \overline{OP} \cdot \cos (\beta - \alpha) $$
Knowing that OA is the distance (d) between the line and the pole, while OP is the length (r):
$$ d = r \cdot \cos (\beta - \alpha) $$
This gives us the formula for the distance we sought to prove.
And so on.
