Equation of a Line Through a Point with a Given Slope

The equation of a line that passes through a specific point P(x₁, y₁) with a given slope m is as follows: $$ y = m \cdot (x - x_1) + y_1 $$ Here, (x, y) represent any other points on the line.

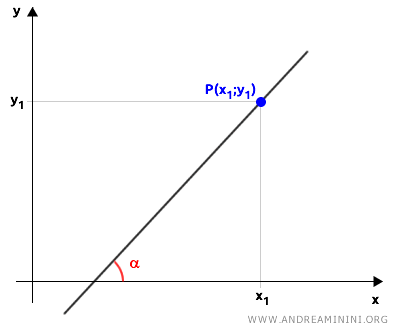
This formula allows us to construct a line starting from a single point (x₁, y₁) if we know its slope.

The slope of a line is its inclination relative to the x-axis.

$$ m = \frac{y - y_1}{x - x_1} $$

It is calculated by finding the ratio of the difference in y-coordinates $ (y - y_1) $ to the difference in x-coordinates $ (x - x_1) $, which measures how steep the line is relative to the x-axis.

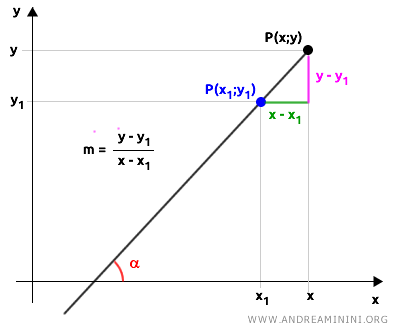
Here, $ m $ indicates the slope of the line, $ (x_1, y_1) $ are the coordinates of a known point through which the line passes, and $ (x, y) $ are the coordinates of any other point on the same line.

Note. The formula $ y = m \cdot (x - x_1) + y_1 $ is particularly useful for geometrically describing a line in the Cartesian plane, given a reference point and its slope. It is also sometimes written in the equivalent form: $ y - y_1 = m \cdot (x - x_1) $

A Practical Example

Let's consider the point (x₁, y₁) = (1, 3) and the slope m = 2.

We apply the equation of the line passing through the point, given the slope.

$$ y = m \cdot (x - x_1) + y_1 $$

In this case, the coordinates of the point are x₁ = 1 and y₁ = 3, and the slope is m = 2.

$$ y = 2 \cdot (x - 1) + 3 $$

$$ y = 2x - 2 + 3 $$

$$ y = 2x + 1 $$

The variables x and y represent the coordinates of all the other points (x, y) on the line.

Using a table, I can calculate some points on the line other than the initial one.

$$ \begin{array}{c|c} x & y = 2x + 1 \\ \hline -1 & -1 \\ 0 & 1 \\ 1 & 3 \\ 2 & 5 \end{array} $$

In this way, I can calculate the coordinates of all the points on the line passing through the point (1, 3) with a slope of m = 2.

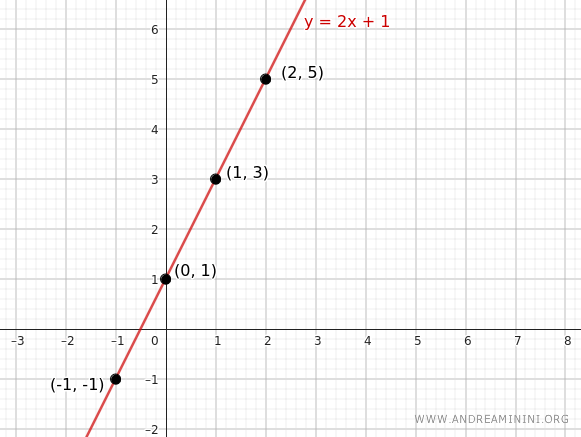
Note. From a geometric standpoint, it is sufficient to know the coordinates of just one other point (x, y) different from the initial point (x₁, y₁) to draw the line passing through the two points. An easy point to calculate is the y-intercept, which is obtained by setting the independent variable x = 0 in the line equation y = 2x + 1.

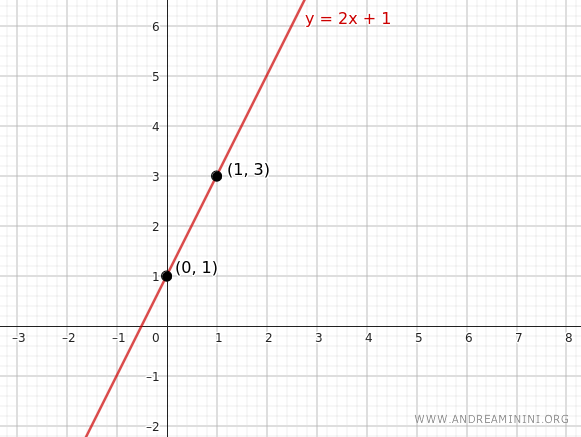
The Proof

This equation is derived from the equation of a line passing through two points (or the condition of the line's alignment).

$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$

With a simple algebraic step, we get:

$$ \frac{y - y_1}{x - x_1} = \frac{y_2 - y_1}{x_2 - x_1} $$

Where $ m = \frac{y - y_1}{x - x_1} $ is the slope of the line.

$$ m = \frac{y - y_1}{x - x_1} $$

Solving for y, we get the equation of the line passing through a point (x₁, y₁) with slope m.

$$ y - y_1 = \frac{m}{x - x_1} $$

$$ y = \frac{m}{x - x_1} + y_1 $$

And so on.