Distance from a Point to a Line

The distance from a point P to a line is the length of the segment connecting point P to the foot of the perpendicular (P').

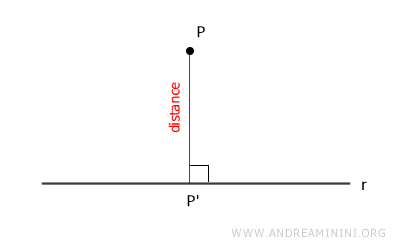
In other words, the distance is the length of the orthogonal projection of the point onto the line.

It's the shortest path from a point to a line. Any other oblique segment from point P to a point on the line is longer than this distance.

The Proof

To prove this, consider any other point on the line different from P', for instance, point A.

The segment AP, which connects points P and A, is oblique relative to the perpendicular.

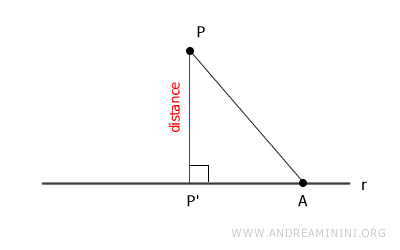
The length of segment AP is definitely greater than the length of segment PP' (the distance), because points P, P', and A form a right triangle.

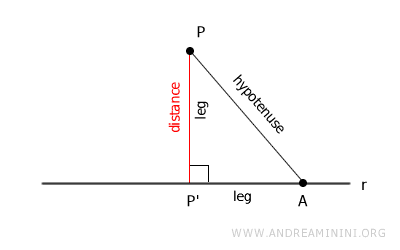
According to the Pythagorean theorem, in a right triangle, each leg is shorter than the hypotenuse.

Therefore, segment AP cannot represent the distance from point P to line r, because the length of segment PP' is always shorter.

This reasoning applies to any segment AP, where A is any point on line r other than P'.

For a deeper understanding of the distance between a point and a line using vector equations, refer to another one of my university notes: how to calculate the distance between a point and a line with vectors. The rest of this note is limited to the plane and the basics of high school analytic geometry.

Calculating the Distance Between a Point and a Line on the Plane

In analytic geometry, the distance between a point P(x₀, y₀) and a line r on the plane is given by this formula: $$ d = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}} $$

Where $ ax + by + c = 0 $ is the general equation of line r, and (x₀, y₀) are the coordinates of point P.

A Practical Example

Consider this line on the Cartesian plane:

$$ 2x + 4y - 6 = 0 $$

and a point A located at the following coordinates:

$$ A \begin{pmatrix} 3 \\ 2 \end{pmatrix} $$

For simplicity, let's plot both point A and the line on the Cartesian plane.

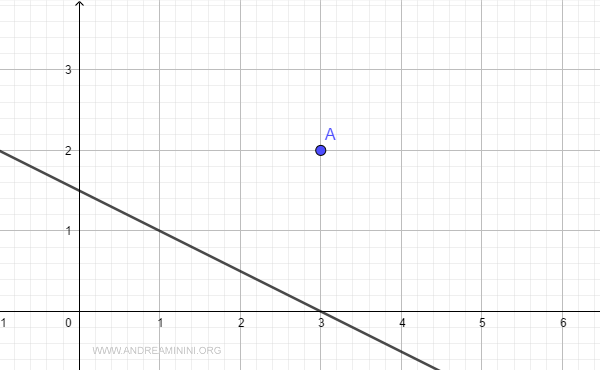
What is the distance between the point and the line?

To find the distance between point A and line r, we use the initial formula:

$$ d = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}} $$

Substitute the coordinates of point A(x₀, y₀) = (3, 2), i.e., x₀ = 3 and y₀ = 2, into the formula:

$$ d = \frac{|a(3) + b(2) + c|}{\sqrt{a^2 + b^2}} $$

Also substitute the coefficients from the general equation of the line $ 2x + 4y - 6 = 0 $, which are a = 2, b = 4, and c = -6:

$$ d = \frac{|2 \cdot 3 + 4 \cdot 2 - 6|}{\sqrt{2^2 + 4^2}} $$

Perform the algebraic calculations:

$$ d = \frac{|6 + 8 - 6|}{\sqrt{4 + 16}} $$

$$ d = \frac{8}{\sqrt{20}} $$

$$ d = 1.78 $$

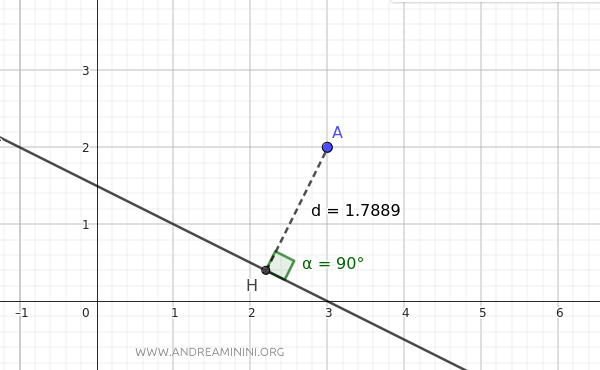
Thus, the minimum distance between point A and the line is 1.78.

A quick check on GeoGebra confirms that the result is correct. The distance d is the segment AH, perpendicular (90°) to the line, with an endpoint at point A(3, 2), and is about 1.78 units long.

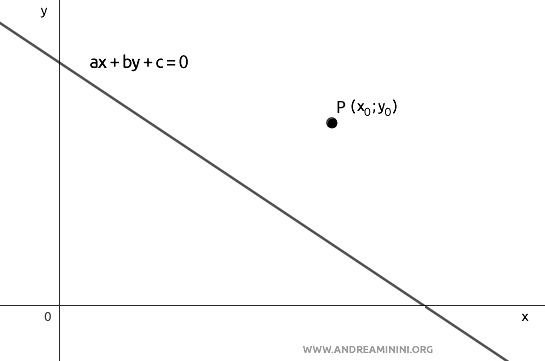
Proof

To prove the distance formula, consider a line $ ax + by + c = 0 $ and any point on the plane $ P(x_0, y_0) $.

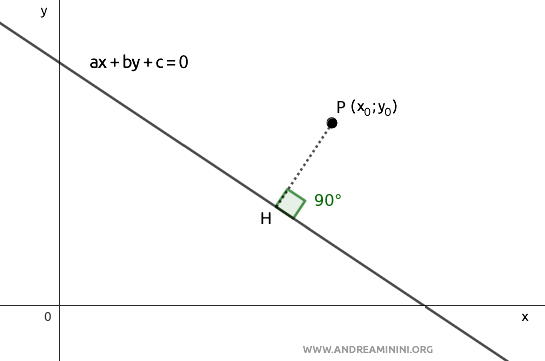
We already know that geometrically the distance is the segment $ \overline{PH} $ perpendicular to the line, with endpoints at point P and a point $ H $ on the line.

Draw two lines parallel to the Cartesian axes passing through point P.

This way, we identify two intersection points A and B with the line.

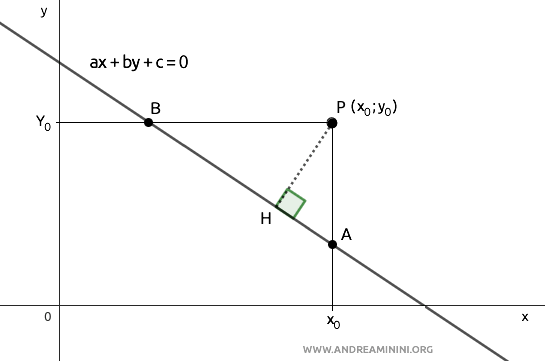
Point A belongs to the line $ ax + by + c = 0 $ and has the same x₀ coordinate as point P.

Thus, we can substitute x with x₀ in the general equation of the line:

$ ax_0 + by + c = 0 $

This allows us to find the value of y:

$$ y = \frac{-ax_0 - c}{b} = - \frac{ax_0 + c}{b} $$

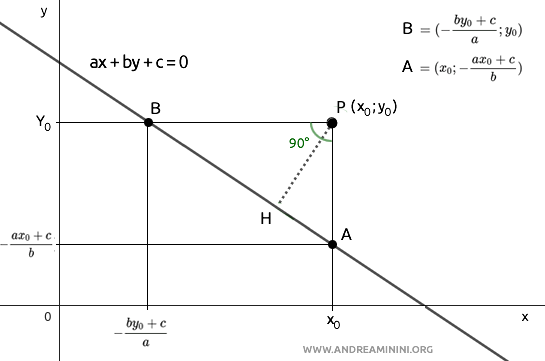
Thus, we obtain the coordinates of point A:

$$ A = ( x_0 ; - \frac{ax_0 + c}{b} ) $$

We apply a similar process for point B.

Point B also belongs to the line $ ax + by + c = 0 $ and has the same y₀ coordinate as point P.

So, we substitute y with y₀ in the general equation of the line:

$ ax + by_0 + c = 0 $

And find the value of x:

$$ x = \frac{-by_0 - c}{a} = - \frac{by_0 + c}{a} $$

Thus, we obtain the coordinates of point B:

$$ B = ( - \frac{by_0 + c}{a} ; y_0 ) $$

In the plane, points A, B, and P form a triangle ABP.

The triangle ABP is a right triangle because its legs coincide with lines parallel to the Cartesian axes, forming a 90° angle.

In a right triangle, the height $ \overline{PH} $ relative to the hypotenuse is equal to the ratio of the product of the legs $ \overline{AP} \cdot \overline{BP} $ to the hypotenuse $ \overline{AB} $.

$$ \overline{PH} = \frac{\overline{AP} \cdot \overline{BP}}{\overline{AB}} $$

Explanation: This formula is derived from the fact that in any triangle, the height is equal to the ratio of twice the area to the length of the base. $$ h = \frac{2 \times \text{area}}{\text{base}} $$ In the case of a right triangle, the area can be calculated using the half-product of the legs, and considering the hypotenuse as the base: $$ h = \frac{2 \times ( \frac{\overline{AP} \cdot \overline{BP}}{2} )}{\overline{AB}} $$ $$ h = \frac{\overline{AP} \cdot \overline{BP}}{\overline{AB}} $$

To find the distance PH, we first need to calculate the lengths of segments AP, BP, and AB.

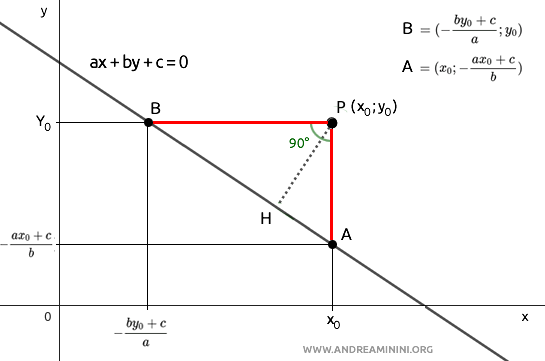
Calculating the lengths of legs AP and BP is straightforward since we know the coordinates of points A and B:

$$ \overline{AP} = | y_0 - ( - \frac{ax_0 + c}{b} ) | = | \frac{ax_0 + by_0 + c}{b} | $$

$$ \overline{BP} =| x_0 - ( - \frac{by_0 + c}{a} ) | = | \frac{ax_0 + by_0 + c}{a} | $$

To calculate the hypotenuse AB, we use the Pythagorean theorem and perform some algebraic steps:

$$ \overline{AB} = \sqrt{\overline{AP}^2 + \overline{BP}^2} $$

$$ \overline{AB} = \sqrt{ ( | \frac{ax_0 + by_0 + c}{b} | )^2 + ( | \frac{ax_0 + by_0 + c}{a} | ) ^2} $$

$$ \overline{AB} = \sqrt{ \frac{(ax_0 + by_0 + c)^2}{b^2} + \frac{(ax_0 + by_0 + c)^2}{a^2} } $$

$$ \overline{AB} = \sqrt{ (ax_0 + by_0 + c)^2 \cdot ( \frac{1}{b^2} + \frac{1}{a^2} ) } $$

$$ \overline{AB} = |ax_0 + by_0 + c| \cdot \sqrt{ \frac{a^2 + b^2}{a^2 b^2} } $$

$$ \overline{AB} = \frac{ |ax_0 + by_0 + c| }{ |ab| } \cdot \sqrt{ a^2 + b^2 } $$

Once we have the lengths of segments AP, BP, and AB, we substitute them into the equation to calculate distance PH:

$$ \overline{PH} = \frac{\overline{AP} \cdot \overline{BP}}{\overline{AB}} $$

$$ \overline{PH} = \frac{ | \frac{ax_0 + by_0 + c}{b} | \cdot | \frac{ax_0 + by_0 + c}{a} | }{ \frac{ |ax_0 + by_0 + c| }{ |ab| } \cdot \sqrt{ a^2 + b^2 } } $$

$$ \overline{PH} = \frac{ | \frac{ax_0 + by_0 + c}{b} | \cdot | \frac{ax_0 + by_0 + c}{a} | }{ \frac{ |ax_0 + by_0 + c| }{ |ab| } \cdot \sqrt{ a^2 + b^2 } } \cdot \frac{ |ab| }{ } $$

$$ \overline{PH} = | \frac{ax_0 + by_0 + c}{b} | \cdot | \frac{ax_0 + by_0 + c}{a} | \cdot \frac{ |ab| }{ |ax_0 + by_0 + c| \cdot \sqrt{ a^2 + b^2 } } $$

Knowing that the absolute value of a product |ab| is equal to the product of the absolute values |a|·|b|,

$$ \overline{PH} = | \frac{ax_0 + by_0 + c}{b} | \cdot | \frac{ax_0 + by_0 + c}{a} | \cdot \frac{ |a| \cdot |b| }{ |ax_0 + by_0 + c| \cdot \sqrt{ a^2 + b^2 } } $$

Furthermore, the absolute value of a ratio is equal to the ratio of the absolute values.

$$ \overline{PH} = \frac{|ax_0 + by_0 + c|}{|b|} \cdot \frac{|ax_0 + by_0 + c|}{|a|} \cdot \frac{ |a| \cdot |b| }{ |ax_0 + by_0 + c| \cdot \sqrt{ a^2 + b^2 } } $$

Simplify to get:

$$ \require{cancel} \overline{PH} = \frac{|ax_0 + by_0 + c|}{\cancel{ |b| }} \cdot \frac{ \cancel{ |ax_0 + by_0 + c| } }{\cancel{ |a| }} \cdot \frac{ \cancel{|a|} \cdot \cancel{|b| } }{ \cancel{|ax_0 + by_0 + c|} \cdot \sqrt{ a^2 + b^2 } } $$

We obtain the desired distance formula between the point and the line:

$$ \require{cancel} \overline{PH} = \frac{|ax_0 + by_0 + c| }{ \sqrt{ a^2 + b^2 } } $$

And so, we have our proof.