Parallel Lines
Two lines are parallel lines if they do not intersect at any point or if they coincide.
The symbols // or || are used to indicate two parallel lines.
$$ r // s $$ $$ r \parallel s $$
The region between the two lines is called a "strip" or "band."
The minimum distance from any point on one line to the other parallel line is known as the "height of the strip" or the distance between the parallel lines.
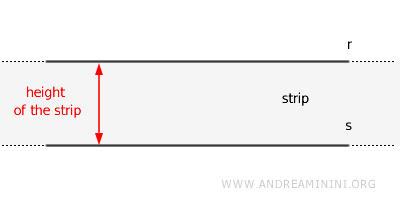
This height represents the perpendicular distance between the two lines and remains constant at every point along each line.
Note. The region between two distinct parallel lines $ r $ and $ s $ can also be described as the intersection of the half-plane bounded by $ r $ that contains $ s $, and the half-plane bounded by $ s $ that contains $ r $.
Euclid’s Fifth Postulate
Given a point $ P $ not lying on a line $ r $, there exists exactly one line $ s $ such that $ s \parallel r $.
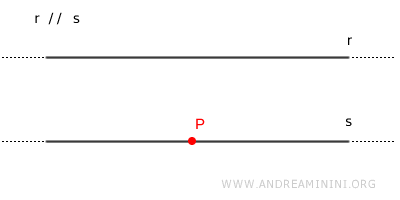
Euclid’s fifth postulate, commonly referred to as the parallel postulate, is the most well-known - and historically the most debated - of his axioms.
Unlike the other four, it is not immediately self-evident or intuitively obvious.
More precisely, it is possible to prove that a line parallel to $ r $ passes through a point $ P $ outside of it, but it is not possible to prove that this line is the only one.
What can be deduced from the postulate?
A number of geometric properties of parallel lines follow directly from the postulate.
- Transitivity Theorem for Parallel Lines
Two lines a and b parallel to a third line c are also parallel to each other (a || b) $$ a \parallel c \ , \ b \parallel c \ \Rightarrow a \parallel b $$Proof. To prove this, we use a contradiction. Assume lines a and b are both parallel to line c but lines a and b are not parallel to each other $$ a \parallel c $$ $$ b \parallel c $$ If lines a and b are not parallel, they intersect at a point P.
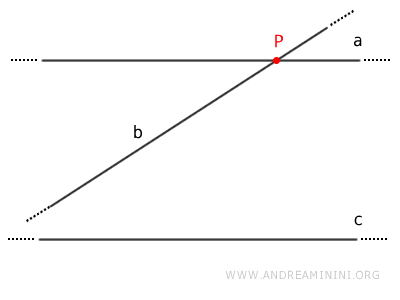
However, according to the initial hypothesis, both lines a and b are parallel to line c. This means that two lines (a and b) pass through point P and are parallel to line c, which is impossible because it contradicts the parallel postulate. Therefore, lines a and b cannot intersect. Thus, the initial statement is false. Its negation is true, meaning lines a and b are both parallel to line c and are also parallel to each other (a//b)
- Parallelism as an Equivalence Relation
The set of all lines parallel to a given line $r$ is known as a direction. This set forms an equivalence class, since each line in the group is parallel to the others, collectively forming a pencil of lines. Therefore, the relation of parallelism among lines qualifies as an equivalence relation, as it satisfies the three defining properties: reflexivity, symmetry, and transitivity.- Reflexivity
Any line is parallel to itself. $$ r \parallel r $$Note. This property is inherent in the very definition of parallel lines.
- Symmetry
If line $r$ is parallel to line $s$, then line $s$ is likewise parallel to line $r$. $$ r \parallel s $$Note. This follows directly from the symmetrical nature of the parallelism relation.
- Transitivity
If line $r$ is parallel to line $s$, and line $s$ is parallel to line $p$, then line $r$ must also be parallel to line $p$. $$ r \parallel s \ , \ s \parallel p \ \Rightarrow r \parallel p $$Note. This results from the theorem stating that two lines parallel to the same line are necessarily parallel to each other.
- Reflexivity
- Theorem on a Line Intersecting a Family of Parallel Lines
If a line $ r $ intersects one line $ a $ in an improper family of parallel lines $ a \parallel b \parallel c \dots $, then it must intersect every other line in the family as well.
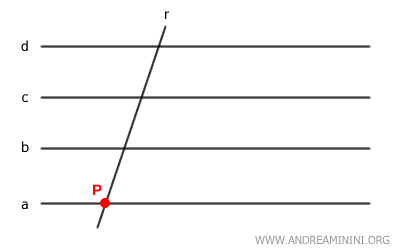
Proof. Consider an improper family of parallel lines: $$ a \parallel b \parallel c \parallel \dots $$ and a line $ r $ that intersects line $ a $ at a point $ P $: $$ r \cap a = \{ P \} $$ We aim to prove that line $ r $ intersects every other line in the family. We proceed by contradiction. Assume that $ r $ does not intersect one of the lines in the family, say line $ b $: $$ r \cap b = \emptyset $$ By definition, this would mean that $ r $ is parallel to $ b $: $$ r \parallel b $$ Since $ b \parallel a $, the transitive property of parallelism would imply that: $$ r \parallel a $$ However, this contradicts our initial assumption that $ r $ intersects $ a $ at point $ P $, since two parallel lines cannot have a point in common. Therefore, the assumption $$ r \cap b = \emptyset $$ must be false. It follows that the contrary holds: $$ r \cap b \ne \emptyset $$ The same argument applies to every other line in the family. Hence, line $ r $ must intersect all the lines in the family.
Necessary and Sufficient Condition for Parallelism Between Two Lines
To determine whether two lines are parallel, two fundamental conditions must be met:
Coplanarity
Two parallel lines must be coplanar - that is, they must lie within the same plane.
Without coplanarity, two lines cannot be parallel.
Thus, coplanarity is a necessary but not sufficient condition for parallelism.
For example, in three-dimensional space, if two lines are not coplanar, they are referred to as skew lines and, by definition, cannot be parallel.
Non-intersection
The two lines must be coplanar and must not intersect.
In other words, beyond being coplanar, the two lines must not intersect - they must have no points in common.
This is the necessary and sufficient condition for two lines to be parallel.
When two lines lie in the same plane and do not intersect at any point, they are necessarily parallel.
Parallel Lines Theorem
If two lines cut by a third transversal line satisfy one of these conditions:
- They form congruent alternate (interior or exterior) angles
- They form congruent corresponding (interior or exterior) angles
- They form supplementary conjugate angles (α+β=180°)
then the two lines are parallel.
This theorem is also known as the parallelism criterion for lines.
The converse is also true: if two lines are parallel, then any transversal will form pairs of congruent alternate angles (interior or exterior), congruent corresponding angles, and supplementary conjugate angles (interior or exterior).
An Alternative Definition
Two lines (not parallel to the y-axis) are parallel if they have the same slope and vice versa.
Practically, two lines are parallel if they have the same inclination with respect to the x-axis.
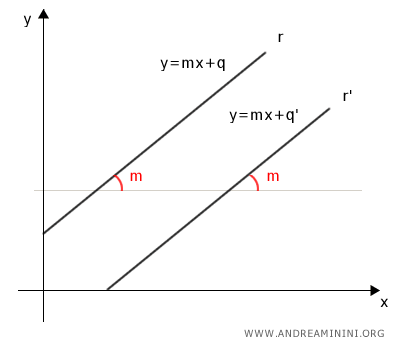
Lines parallel to the y-axis are exceptions because their slope is undefined.
Inverse Theorem. If two lines have the same slope (m=m'), then they are parallel.
A Practical Example and Proof
Consider two parallel lines r:y=2x-2 and r':y=2x-6
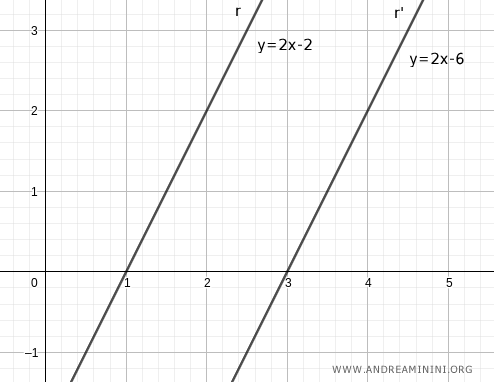
Let x1 and x1' be the points where the lines intersect the x-axis.
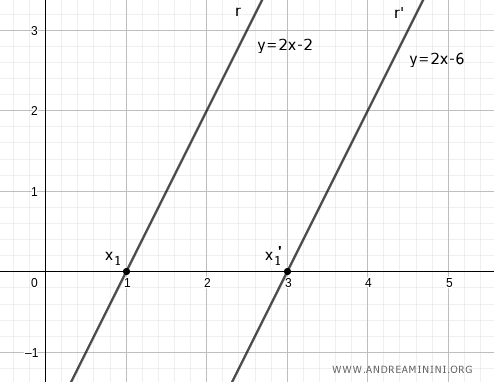
Identify two more points on the x-axis by adding a constant k to x1 and x1'. For instance, let k=1.
$$ x_2=x_1+k $$
$$ x_2'=x_1'+k $$
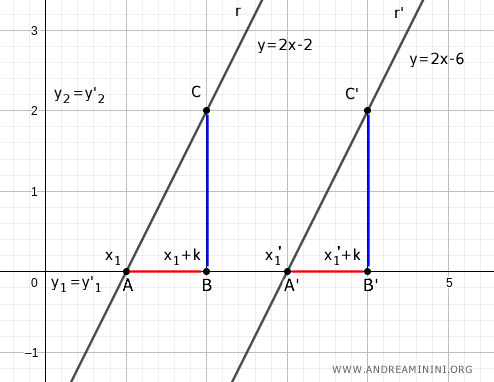
Thus, the two segments x1x2 and x1'x2' are of the same length.
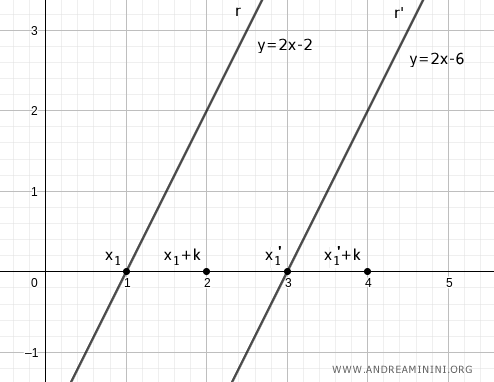
Draw a perpendicular line from x1+k and x1'+k intersecting their respective lines r and r'.
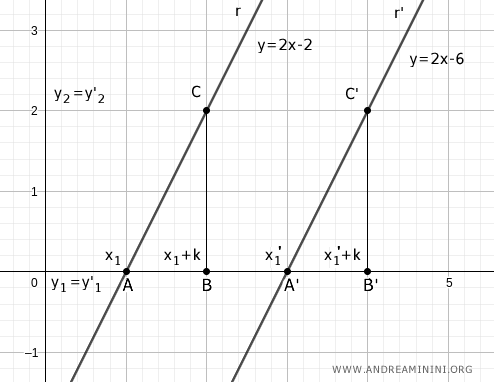
This creates two right triangles, ABC and A'B'C'.
These triangles have the right angles (90°) congruent α=α'.
According to the parallel lines theorem, the angles β=β' are also congruent because they are corresponding angles since parallel lines r and r' are cut by the same transversal (the x-axis).
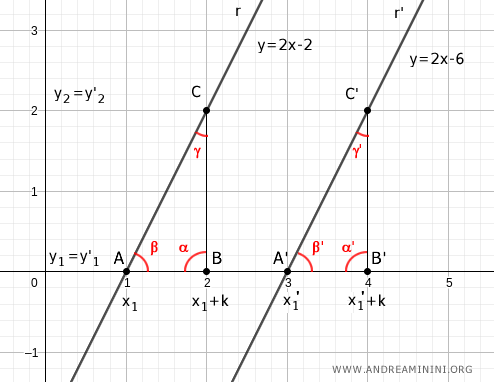
According to the second criterion of congruence, the two triangles ABC≅A'B'C' are congruent because they have one congruent side AB≅A'B' by construction and the adjacent congruent angles α≅α' and β≅β'.
Note. Since these are right triangles, they both have a 90° angle (α=α'). They both have an angle (β=β') determined by the same transversal intersecting the x-axis. Therefore, the third angle must also be congruent (γ=γ') because the sum of the angles in a right triangle is 180°.
The two triangles are congruent ABC≅A'B'C', meaning all their sides are the same length.
Thus, the two legs of the right triangle are congruent.
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
Knowing that AB=x2-x1 and A'B'=x'2-x'1 (where x2=x1+k and x'2=x'1+k) and that BC=y2-y1 and A'B'=y'2-y'1
$$ x_2 - x_1 = x'_2-x'_1 $$
$$ y_2 - y_1 = y'_2-y'_1 $$
The slope is determined by the ratio of the two legs of the right triangle:
$$ m = \frac{y_2-y_1}{x_2-x_1} $$
$$ m' = \frac{y'_2-y'_1}{x'_2-x'_1} $$
Since the sides are equal, the slope is the same.
$$ m = m' $$
Proof of the Inverse Theorem. The reasoning can also be done in reverse. Starting from the hypothesis that two lines with the same slope m=m' can demonstrate that the two lines are parallel.
If two lines have the same slope $$ m=m' $$ since m=BC/AB and m'=B'C'/A'B', the following equality holds $$ \frac{\overline{BC}}{\overline{AB}} = \frac{\overline{B'C'}}{\overline{A'B'}} $$ Where AB and A'B' are segments on the x-axis, while BC and B'C' are segments on the y-axis. If the segments on the x-axis AB≅A'B' are congruent, I find that the segments on the y-axis BC≅B'C' are also congruent.
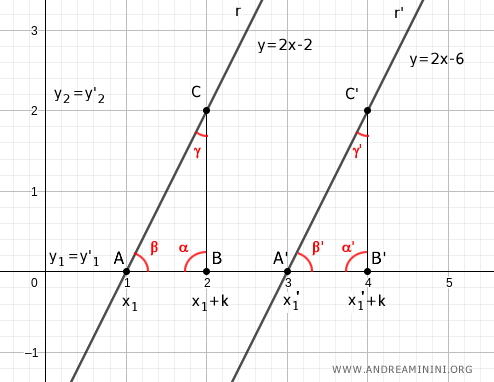
Therefore, the right triangles ABC≅A'B'C' are congruent according to the first criterion of triangle congruence, because they have two congruent sides AB≅A'B' and BC≅B'C' and the angle between them α≅α' (90°) congruent. Consequently, the triangles ABC≅A'B'C' have all the same angles. In particular, I am interested in knowing that the angles β≅β' are congruent because they measure the inclination of the lines r and r' concerning the x-axis, as this allows me to deduce that the two lines have the same inclination regarding the x-axis, i.e., they are parallel lines r // r'.
The Condition for Parallelism of Lines
Two lines $ r $ and $ s $ with the following equations in implicit form $$ r: \ ax+by+c=0 $$ $$ s: \ a'x+b'y+c'=0 $$ are parallel $ r // s $ if the coefficients of the equations satisfy the following condition $$ ab' - a'b = 0 $$ which can also be written in this equivalent form $$ \frac{a}{a'} = \frac{b}{b'} $$
This condition is known as the parallelism condition for lines.
Example
Consider an example of two parallel lines $ r // s $ with the following equations in implicit form:
$$ r: \ 2x+3y+1=0 $$
$$ s: \ 4x+6y-8=0 $$
Let's verify if the two lines satisfy the parallelism condition.
$$ ab' - a'b = 0 $$
In this case, a=2, b=3, a'=4, and b'=6.
$$ 2 \cdot 6 - 4 \cdot 3 = 0 $$
$$ 12 - 12 = 0 $$
The parallelism condition is satisfied, so the two lines are parallel $ r // s $.
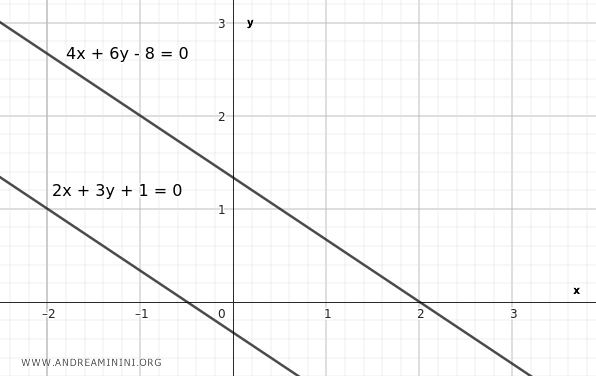
Proof
Consider two parallel lines $ r // s $ with the following equations in implicit form:
$$ r: \ ax+by+c=0 $$
$$ s: \ a'x+b'y+c'=0 $$
The slopes of the two lines are:
$$ m = - \frac{a}{b} $$
$$ m' = - \frac{a'}{b'} $$
Since the lines are parallel by the initial hypothesis, the two slopes are equal:
$$ m = m' $$
$$ - \frac{a}{b} = - \frac{a'}{b'} $$
With a few simple algebraic steps, we get the parallelism condition between the lines:
$$ \frac{a}{b} = \frac{a'}{b'} $$
$$ ab' = a'b $$
And this concludes the proof.
How to Determine if Two Lines are Distinctly Parallel or Coincident
Two lines are distinctly parallel if their equations satisfy the parallelism condition but do not satisfy the coincidence condition. $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$ Conversely, if they satisfy both conditions, they are coincident lines. $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$
Both distinctly parallel lines and coincident lines satisfy the parallelism condition:
$$ \frac{a}{a'} = \frac{b}{b'} $$
Where a,a',b,b' are the coefficients of the variables x and y in the two lines:
$$ r: ax+by+c=0 $$
$$ r': a'x+b'y+c'=0 $$
In other words, coincident lines are a special case of parallel lines because they have the same slope.
To determine if two parallel lines are distinct or coincident, we must also analyze the coincidence condition by examining the ratio of their constant terms $ \frac{c}{c'} $ .
- Coincident
If the ratio of the constant terms is proportional to that of the coefficients, then the lines are coincident, meaning they have all points in common: $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$ - Distinctly Parallel
If the ratio of the constant terms is different from that of the coefficients, then the lines are distinctly parallel, meaning they do not intersect at any point: $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$
Example
Consider two lines with the following improper form equations:
$$ r:2x+3y+6=0 $$
$$ r′:4x+6y+12=0 $$
We need to determine if they are intersecting, parallel, or coincident.
First, let's check if the parallelism condition is satisfied:
$$ \frac{a}{a'} = \frac{b}{b'} $$
In this case, the coefficients of the variables x and y are a=2, b=3 in the first equation, and a'=4, b'=6 in the second equation.
$$ \frac{2}{4} = \frac{3}{6} $$
$$ \frac{1}{2} = \frac{1}{2} $$
The parallelism condition is satisfied, so we know for sure that the two lines are not intersecting.
However, we need to determine if they are distinctly parallel or coincident.
To do this, we analyze the coincidence condition by examining the ratio of the constant terms c=6 and c'=12 of the two equations:
$$ \frac{c}{c'} = \frac{6}{12} = \frac{1}{2} $$
All the ratios are equal to 1/2, so the two lines are coincident:
$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{1}{2} $$
In other words, the two lines have all points in common.
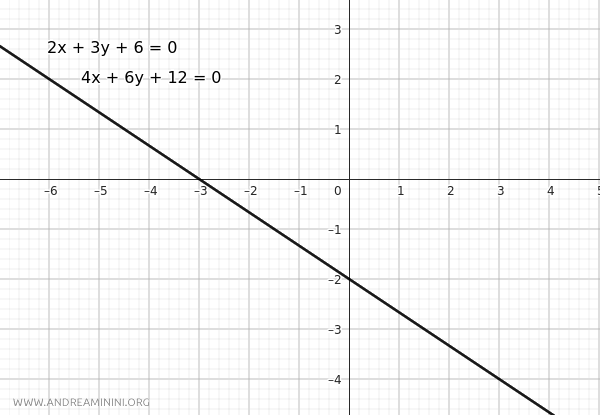
These simple steps allow us to accurately determine the relationship between two lines based on their coefficients without solving a system of equations.
Example of Distinctly Parallel Lines. For completeness, let's consider another example where two lines are distinctly parallel. Take these two lines: $$ r:2x+3y+6=0 $$ $$ r′:4x+6y+3=0 $$ The equations are similar to the previous example. The parallelism condition is satisfied: $$ \frac{a}{a'} = \frac{b}{b'} $$ $$ \frac{2}{4} = \frac{3}{6} $$ $$ \frac{1}{2} = \frac{1}{2} $$ However, in this case, the coincidence condition is not satisfied because the ratio of the constant terms is equal to 2: $$ \frac{c}{c'} = \frac{6}{3} = 2 $$ So the ratio c/c' of the constants is not proportional to the ratio of the variable coefficients: $$ \frac{a}{a'} = \frac{b}{b'} = \frac{1}{2} \ne 2 = \frac{c}{c'} $$ Therefore, the two lines are distinctly parallel.
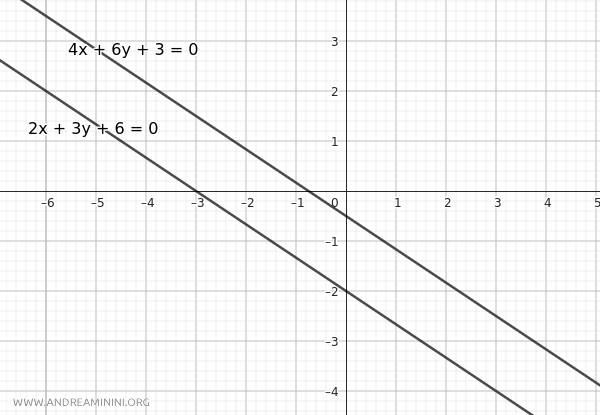
Observations
Some observations about parallel lines:
- The distance between two parallel lines is constant at every point along each line
If you draw perpendicular segments from any two points on a line $r$ to a second line $s$ that is parallel to $r$, those segments will be congruent.
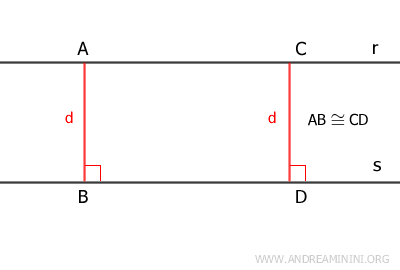
In other words, the distance between two parallel lines is uniform - no matter which point you choose, the perpendicular segment connecting the lines will always have the same length.Proof. If we consider two parallel lines r // s, since lines perpendicular to one line are also perpendicular to the other, if we take two segments AB and CD perpendicular to the lines r and s, they form a rectangle ABCD. In a rectangle, the opposite sides are congruent, so the segments AB≅CD are congruent. This proves that the distance (height) between two parallel lines is constant at any point.
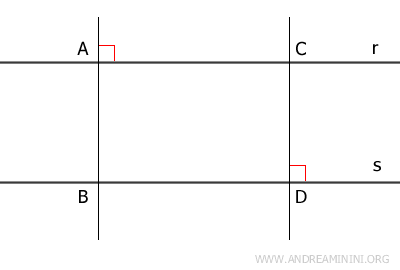
Alternative proof. Take two parallel lines $r$ and $s$. Select any two distinct points $A$ and $C$ on line $r$ and drop perpendiculars from these points to line $s$, intersecting at points $B$ and $D$. Now draw the segment $AD$.
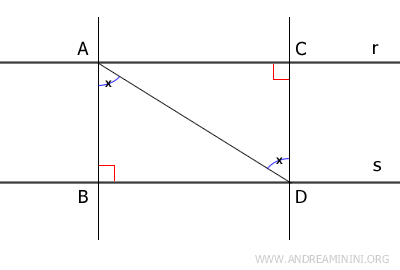
The triangles $ \triangle ABD $ and $ \triangle ACD $ are congruent by the Angle - Side - Angle (ASA) congruence criterion. They share the side $AD$, both contain a right angle, and they have a pair of congruent alternate interior angles formed by a transversal intersecting parallel lines. As a result, all corresponding sides are congruent, including $AB \cong CD$. This confirms that the distance between parallel lines remains constant at every point along the lines. - Two lines r and s perpendicular to a third line t are parallel
Lines r and s form pairs of congruent corresponding angles. Therefore, according to the parallel lines theorem, they are parallel.
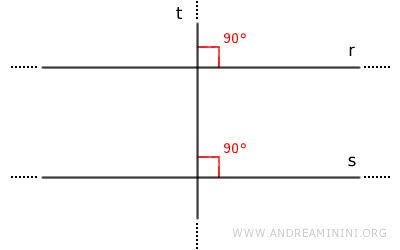
Alternatively, one can note that r and s form congruent alternate interior (or alternate exterior) angles, or supplementary same-side interior angles. In each of these cases, the result is the same: r and s must be parallel.Proof. Let $r$ and $s$ be two lines perpendicular to the same line $t$. Assume, for contradiction, that $r$ and $s$ intersect - in other words, that they are not parallel. Then they would meet at some point $P$. But this would imply that two distinct lines, both perpendicular to $t$, pass through the same point $P$, which contradicts the uniqueness of the perpendicular. Therefore, the assumption is false, and we conclude that $r$ and $s$ are parallel.
- Parallel Postulate (Euclid's Fifth Postulate)
Given a point P outside of line r, there is exactly one line that runs parallel to r.
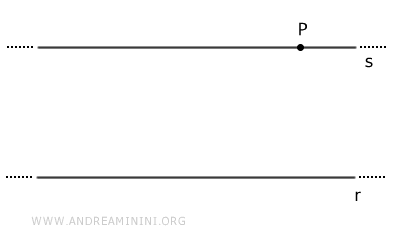
- A line t perpendicular to line r is also perpendicular to all lines parallel to r
Given two parallel lines r and s, if line t is perpendicular to one line, it is also perpendicular to the other.
Proof. Consider two parallel lines r//s and a third line t perpendicular to line s. According to the initial hypothesis, lines t and s form a right angle α=90°.
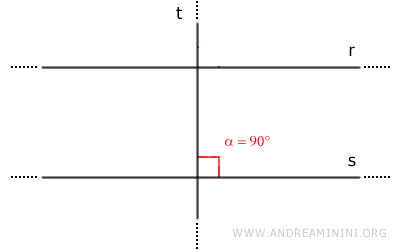
Lines r and s are parallel lines r//s. According to the parallel lines theorem, lines r and s form two pairs of congruent corresponding angles with the same transversal line (α≅β). Therefore, angle β is also a right angle (β=90°).
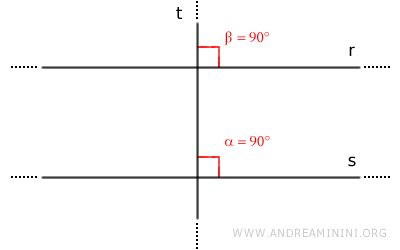
Consequently, line t is also perpendicular to line r. - The parallel lines of two intersecting lines a and b are also intersecting
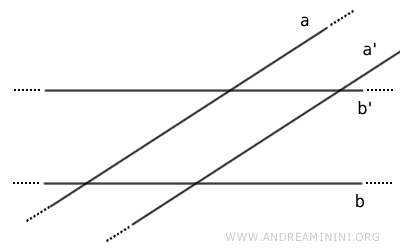
Proof. By contradiction, given two intersecting lines a and b, their respective parallel lines a' and b' are parallel to each other a' // b' $$ a \parallel a' $$ $$ b \parallel b' $$ $$ a' \parallel b' $$ If lines a' and b' are parallel to each other (a' // b'), according to the transitive property, lines a // b would also be parallel $$ a' \parallel b' \ , \ b' \parallel b \Rightarrow a \parallel b $$ However, this contradicts the initial hypothesis that lines a and b are intersecting. Thus, the statement is false. Its contrary is true, meaning given two intersecting lines a and b, their respective parallel lines a' and b' are also intersecting.
- Theorem of Parallel Planes Intersected by a Third Plane
When a plane \( \pi \) intersects two parallel planes \( \pi_1 \) and \( \pi_2 \), the intersections form two parallel lines.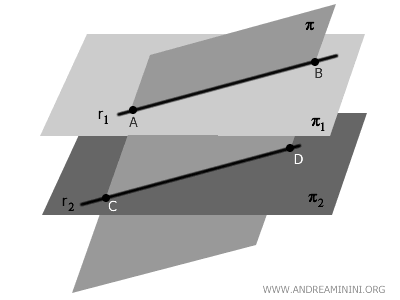
This happens because when a plane \( \pi \) cuts through two parallel planes \( \pi_1 \) and \( \pi_2 \), the intersections create two lines \( r_1 \) and \( r_2 \). Since \( \pi_1 \) and \( \pi_2 \) are equidistant and \( \pi \) intersects them at the same angle, the lines \( r_1 \) and \( r_2 \) are guaranteed to be parallel.
And so on.
