Theorem of Parallel Planes Intersected by a Third Plane

When a plane $ \pi $ intersects two parallel planes $ \pi_1 $ and $ \pi_2 $, the intersections are two parallel lines $ r_1 $ and $ r_2 $.
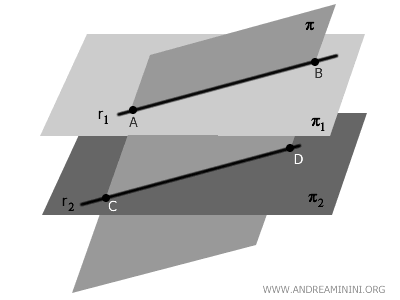
proof

This happens because $ \pi_1 $ and $ \pi_2 $ are parallel and equidistant, so the plane $ \pi $ cuts through them, forming two lines $ r_1 $ and $ r_2 $.

Since $ \pi $ meets both planes at the same angle, the lines $ r_1 $ and $ r_2 $ are parallel to each other.

Proof

Let us examine two parallel planes $ \pi_1 $ and $ \pi_2 $.

By definition, the distance between $ \pi_1 $ and $ \pi_2 $ remains constant, and their normal vectors are proportional.

A third plane $ \pi $ intersects $ \pi_1 $ along the line $ r_1 $ and $ \pi_2 $ along the line $ r_2 $.

proof

Because $ \pi_1 \parallel \pi_2 $, the plane $ \pi $ intersects both planes while maintaining the same angle of intersection.

The lines $ r_1 $ and $ r_2 $ lie within the same plane $ \pi $, which makes them coplanar.

Now, consider two points $ A $ and $ B $ on $ r_1 $, and their corresponding projections $ A' $ and $ B' $ on $ r_2 $.

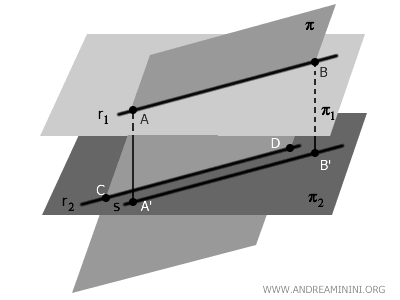
example

The perpendicular segments $ AA' $ and $ BB' $ represent the constant distance between $ \pi_1 $ and $ \pi_2 $. As a result, these segments are both parallel and congruent.

$$ AA' \parallel BB', \quad AA' \cong BB' $$

Since the geometry of the plane $ \pi $ ensures that $ r_1 $ and $ r_2 $ maintain the same orientation, it follows that $ r_1 \parallel r_2 $ by definition.

In conclusion, the lines $ r_1 $ and $ r_2 $ are parallel because they lie in the same plane $ \pi $, share the same orientation, and respect the constant separation between $ \pi_1 $ and $ \pi_2 $.

And so forth.